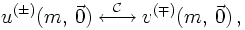The Dirac equation

The real thing

1. Charged spin-½ particles: Two spinors
   

   REPRESENTATION OF PARTICLES WITH SPIN ½

   From the reasoning above, it is clear that particles with spin ½ are represented best by spinors, i.e. by objects χ where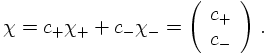 It should be noted here that the last step above implies that the two spin eigenstates χ(\plusmn;) depend on a choice of axis for the Stern-Gerlach type experiment with which the spin can be measured. The states χ(±) then refer to those states with eigenvalue ±½. It is clear that a rotation of this axis implies a change of the eigenbasis, which cannot be connected to usual rotation matrices, cf. the representation here. Therefore, a particle with spin ½ cannot be represented by a complex scalar field, since in such a field the two components do not mix under rotations and the field thus has a different behaviour under Lorentz transformations.
   It should be stressed here that spin is just some internal degree of freedom, not necessarily connected to electric charges of the particle in question. For instance, the neutrinos ν are spin-½ particles, and they can be repesented by such spinor fields. At this point it should be noted however that since they do not have electric charges, it is tempting to identify them with their own anti-particles (more on this later). This connects the conjugated spinors with the original ones and leads to fields known as Majorana particles.
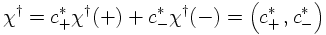
   To summarize: A field with spin ½ is described by a spinor with two components, one for each spin. Since the two spins form a complete basis, linear combinations of the two basic spinors describe this particle. To rotate the basis around some axis, transformations along the reasoning of the equations above must be employed.
   
   A final remark is in order here: When analysing the Lorentz group it becomes apparent that it can be written as a product of two groups, Clearly, the Pauli matrices σ are the generators of these groups. As has been seen before, two-component spinors are suited for the description of particles in such a representation of one of the groups. So, usually the two SU(2) groups are represented by two sets of Pauli matrices, one of them with dotted and the other one with undotted indices. In other words, the generators look like where Accordingly the corresponding spinors have either dotted or undotted components, depending on whether they transform under the dotted or the undotted SU(2).
   
   

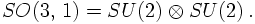
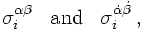
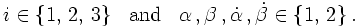
   INCLUDING CHARGES

   So far, a representation of spin-½ particles without charges has been constructed. The complex scalar field now serves as a spin doctor to answer the question how to include charges into the description of spin-½ particles. In the case of scalar fields, the number of degrees of freedom has been doubled: Starting from one neutral real field, a charged complex field has been constructed. In the case of spin-½ particles, however, it is not sufficient to make the components complex numbers. Instead, rather the number of components needs to be doubled. This also ensures the trivially correct behaviour under rotations, keeping the respective components for the different charges separate.
   In other words, such particles can be represented by a bi-spinor, an object that consists of two spinors. In this framework these individual spinors are usually denoted η and ξ having dotted and undotted components, respectively. An ordinary (Dirac-) bi-spinor consists of two such spinors, They transform under their respective SU(2) group, either the dotted or the undotted one.
   
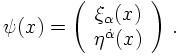
   In practise, however, these Dirac-spinors are often expanded in terms of another spinor basis with four entries for each base spinor. These spinors are commonly denoted by u and v, respectively, and they are meant to carry opposite charges. The connection of otherwise identical particles with opposite charge and the particle anti-particle relation will be discussed later. In a suitable basis these solutions read, up to a normalisation constant N, for the (anti-)particle at rest.
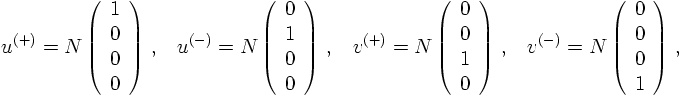
   As mentioned before, the idea now is to identify the u- and v-solutions with degrees of freedom carrying opposite charge. In the case of the complex scalar field, this charge conjugation has been achieved by complex conjugation, for spinors the procedure is a bit more complicated: After all, the u and the v pieces have to be interchanged.
   
   

   CHARGE CONJUGATION

   In the absence of other (gauge) fields, the operation of charge conjugation will connect the u and the v solutions in the following way: where the arguments of the spinors, having mass m, indicate that this holds true for particles at rest. It is worth noting that the operation of charge conjugation also flips the spins: any u spinor with positive spin is transformed into a v-spinor with negative spin. Later on, the exact form of the charge conjugation operator C will be constructed. But before this, the spinors constructed so far will be put into the context of dynamical theories.
   
   
2. Linearisation
   
3. Equation of motion for particle and antiparticle
   
4. Relativistic invariance: The Dirac algebra
   
5. Spin, helicity and chirality
   
6. The parity of the Dirac spinors
   
7.