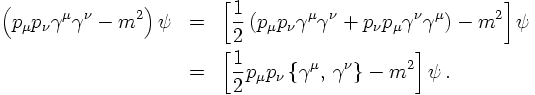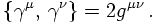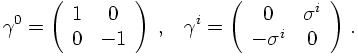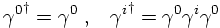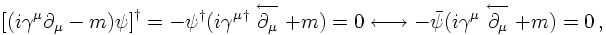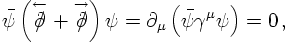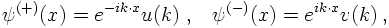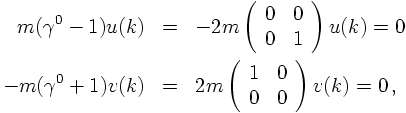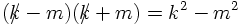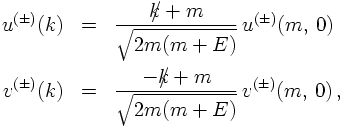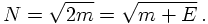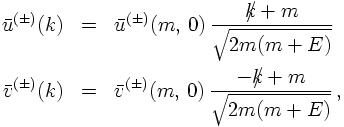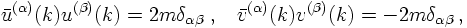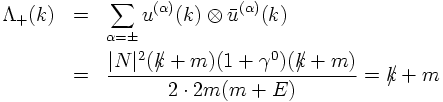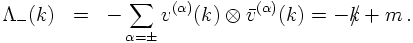Relativistic invariance: The Dirac algebra
CONNECTION TO KLEIN-GORDON EQUATION
Multiplying the second equation from the left with the operator of the first (or vice versa) yields
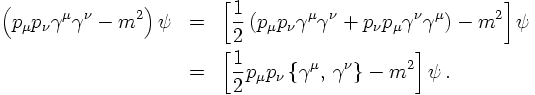The resulting operator becomes the kernel of the Klein-Gordon equation only, if
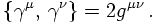This infact defines the γ matrices. An explicit representation in terms of the Pauli
matrices and the unit matrix is given by
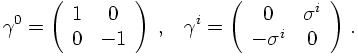Since, after explicit calculation in this representation,
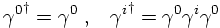the E.o.M. for the daggered spinor can now be obtained from the one for the undaggered one:
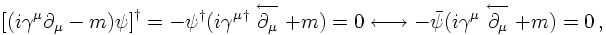as before. The trick here was to multiply from the right with γ0 in the last step.
CURRENT AND CHARGE
Combining the E.o.M. for the barred and the unbarred spinors, i.e. adding them, yields
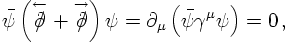a perfect candidate for a conserved current. The corresponding density is positive, by construction,
and therefore perfectly suited to describe a particle density. Needless to stress that the current
transforms like a four-vector.
STATES
In a next step, let's try to construct plane wave solutions of the Dirac equation with positive or
negative energies: Both signs should appear, after all, the Dirac equation is a linearisation of the
Klein-Gordon equation involving more degrees of freedom, but it should now be possible to map
the different energy signs onto specific solutions. So, for this case, let's try an ansatz of the
form
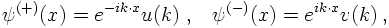where the signs in the superscript indicate the sign of the energy. The Dirac equation now implies that
for particles at rest the two solutions must satisfy
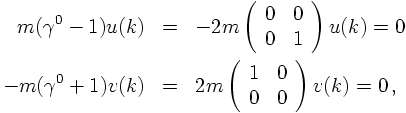where the entries in the matrices are to be understood as 2x2 matrices. This shows that the solutions
given above for the eigenstates are indeed deeply rooted in the form of the E.o.M.s.
Starting form these solutions for the particles at rest, it would be simple to perform a boost in
order to obtain the solutions for the particles moving. However, rather than so doing, it is simpler
to observe that
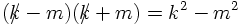and to write
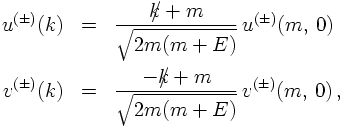where in both cases E is defined as the corresponding positive quantity. Now, it is time to
specify the normnalisation factor N in front of the spinors at rest. It will turn out that
a convenient choice is
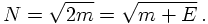The latter identity of course holds true only for particles at rest, where E = m.
For the conjugate spinors similar equations hold true, i.e.
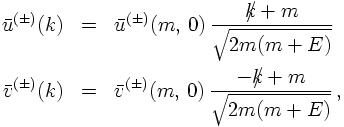implying that the base states are orthogonal with norm N:
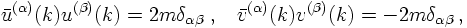with all other combinations vanishing. The quantisation of the Dirac field proceeds in the usual
way: For each degree of freedom a corresponding creation operator is introduced; their complex
conjugates being the annihilation operators. Therefore, altogether four creation operators
are defined, which are multiplied with "their" respective spinor component and a plane wave
factor. However, this will not be discussed here in great detail.
PROJECTORS ON POSITIVE OR NEGATIVE ENERGIES
Consider now the matrices
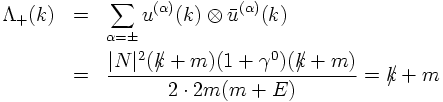and similarly for the negative energy states,
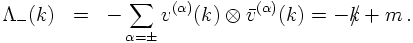They serve as projectors onto positive and negative energy states. Their sum equals 2m,
squaring them results - up to a factor of 2m - in the original projector.