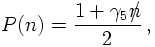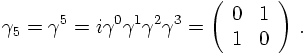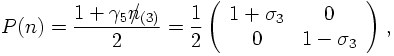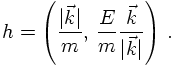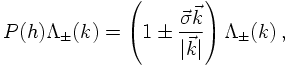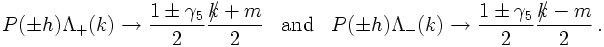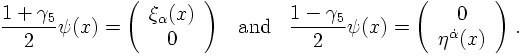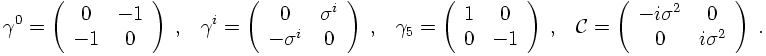The Dirac equation

The real thing

1. Charged spin-½ particles: Two spinors
   
2. Linearisation
   
3. Equation of motion for particle and antiparticle
   
4. Relativistic invariance: The Dirac algebra
   
5. Spin, helicity and chirality
   

   SPIN OF THE SPINORS

   Spins of the spinor fields are measured through a projection operator P(n), incorporating the normalised reference axis n, which is orthogonal to the momentum k, 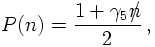where the new matrix reads 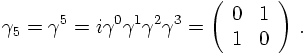P(n) projects onto the state, which in its rest frame has a spin of ±½ for positive/negative energy solutions. This becomes explicit when choosing n along the z-axis, i.e. n=(0,0,0,1). The projector then reads 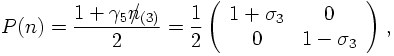and the various rest-frame solutions u and v are eigenstates of this operator with eigenvalues +½ for the spin-up pieces and -½ for the spin-down pieces.
   
   

   HELICITY

   Clearly, the definition of spin depends on the choice of some axis outside of the particle itself. Let us instead try to find another set of states that does not depend on some external, in principle arbitrary, axis. Such a definition of states is provided by the helicity, which uses a special axis n, namely 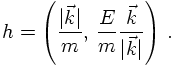Therefore, the helicity axis basically points into the direction of motion of the particle. With this definition, 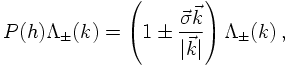i.e. the projector w.r.t. the helicity h projects onto positive energy, positive helicity and negative energy, negative helicity states. It should be noted here that the operator kσ commuts with the momentum operator, both can thus be measured simultaneously. Also, in the ultrarelativistic (massless) limit 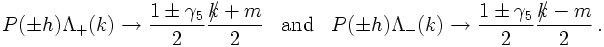Anyways, it should be clear by now that instead of labelling the states by their spin, it is also possible to label them through thier helicity, which also forms a complete basis.
   
   

   CHIRALITY

   Chirality is yet another way to look at this. States labelled by chirality are defined through the eigenvalues of the the chirality operator 1±γ₅.
   It is tempting now to perform a base transformation of the spinors and the γ matrices such that the chirality operator projects onto upper and lower components of the spinor, namely 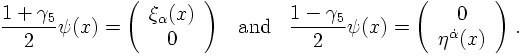This would imply that these two components, related to different subgroups of the Lorentz group can be decoupled, and for instance, could behave differently under interactions. To do so, yet another representation of the &gamma, matrices needs to be constructed. It is called the chiral basis and is given by 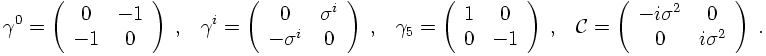It turns out that this basis is much more suited to investigate some more properties of the spinors. For instance, it can be shown that for massless particles - or in the ultrarelativistic limit - helicity equals chirality.
   
   
6. The parity of the Dirac spinors
   
7.