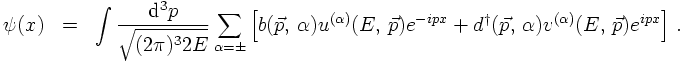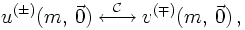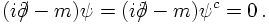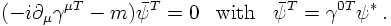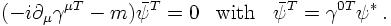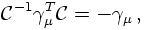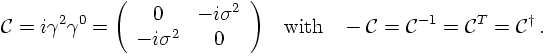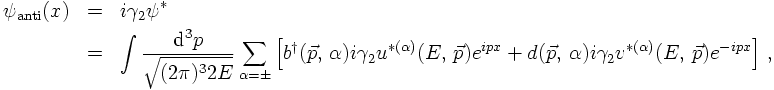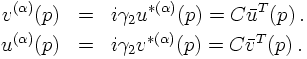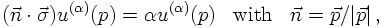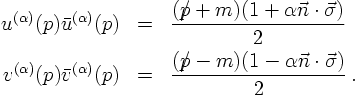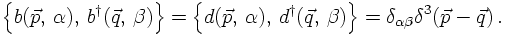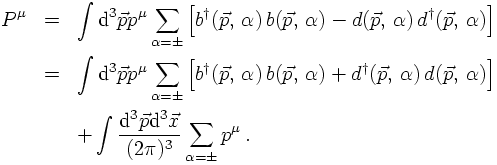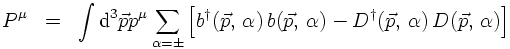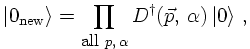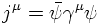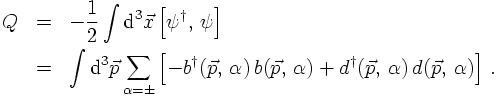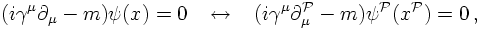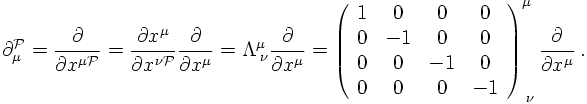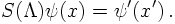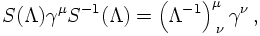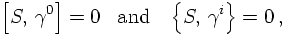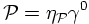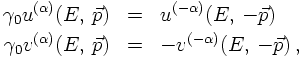The parity of the Dirac spinors
QUANTISATION
Following the usual procedure of quantising a field by introducing suitable creation operators
and multiplying them with the corresponding degree of freedom and a plane wave factor, the
Dirac field operator for the particle reads
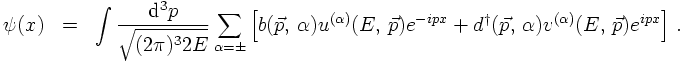It should be understood that the sum over α denotes either a sum over spins or over
helicities - whatever is better suited. This is possible since both the spin and the helicity
eigenstates form a complete basis. Here and in the following, always the helicities are chosen.
The field operator for the anti-particle can be obtained by complex conjugation. There is one
subtlety, however, namely that the anti-particle should have opposite charge w.r.t. the original
particle. In order to do so, the operation of chare conjugation must be scrutinised first.
CHARGE CONJUGATION RELOADED
Now it is time to reconsider the charge conjugation operation. Previously it has been
mentioned that under charge conjugation the u and the v components are transformed into each
other,
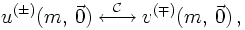now it is time to quantify this a bit. Let us define first that charge conjugation leaves
the free E.o.M. invariant, i.e. they are identical for particles and their charge-conjugate
counterpart:
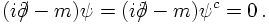differences should occur only, when the spinors are coupled to a gauge field, like, e.g. the
electromagnetic field. Clearly then, the sign of the interaction should change for the charge-conjugated
field. However, how can now the two fields, the original one and the charge-conjugated be connected?
To answer this, take the equation for the barred spinor and transpose it. The result reads
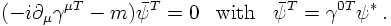The charge conjugation matrix is now the matrix which fulfils
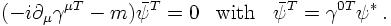leading to
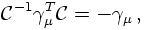Therefore, the charge conjugate can be identified as the barred and transposed spinor,
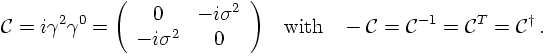It should be noted here that due to the fact that spinors describe anticommuting fermions,
the operation of charge conjugation changes the sign of the current defined above.
Therefore, the field operator for the anti-particle now reads
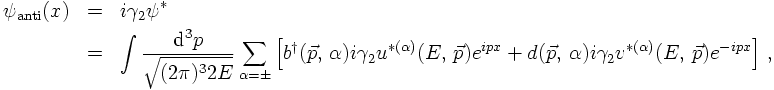making the connection of the u and the v base spinors even more explicit. In fact,
comparing the two field operators results in
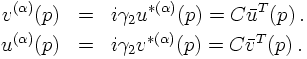It is easy to check that these relations go perfectly along the E.o.M. for the base spinors.
PARTICLE-HOLE INTERPRETATION
Using helicity to label the states,
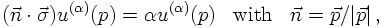products of the base vectors without summation can be calculated, yielding
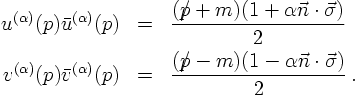Using them as projectors and applying them to the field operators shows that the creation and
annihilation operators b and d indeed fulfil anti-commutation relations in momentum space, i.e.
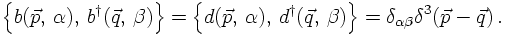This establishes that the Dirac equation is quantised with help of anti-commuting operators,
and thus describes fermions.
The momentum operator can be constructed in the usual way. It reads
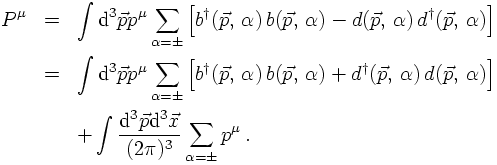In the last transformation Dirac's idea (the particle-hole theory) is encoded in a very short
and elegant form: When quantising the theory, the operators b and d have been identified as
annihilation operators of positive and negative energy states, respectively. Identifying instead
d as creation operator (and, to make the re-interpretation manifest, replacing it by
D†), the first line of the equation above reads
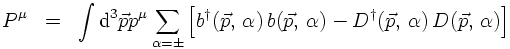and, obviously the corresponding creation operator creates a particle with momentum -p. Constructing
a new vacuum, which instead of containing no particles now contains all particles created by the
D† operators (creators for negative energies),
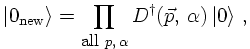then the corresponding annihilation operators D acting on this vacuum do not annihilate it but
rather leave a particle state. Rephrased in terms of the original operators: Any d†(p)
acting on this sea of negative energy solutions marking the new vacuum leads to a hole in the
sea with momentum -p. In this framework the c-number in the second line of the momentum operator
above is nothing but the (negative) energy of the sea-vacuum. When comparing this with the
vacuum-energy of an harmonic oscillator, which is positive, one is tempted to state that bosonic vacua
have positve nergies and fermionic ones have negative energies. This is of some importance in the
construction of supersymmetric field theories.
From the definition of the current of the Dirac field,
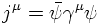the charge can be obtained. After anti-symmetrisation it reads
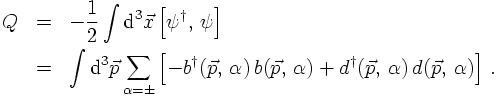Therefore the operators b† and d† create particles with charge
Q = -1 and Q = +1, respectively.
PARITY OF THE SOLUTIONS
Let's now investigate the behaviour of the Dirac spinor under parity transformations, i.e.
under spatial reflections (t,x)→(t,-x). In other words, a transformation of the solutions
ψ of the Dirac equation needs to be constructed such that it solves the parity-transformed
Dirac equation:
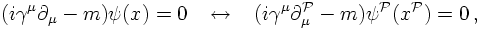where
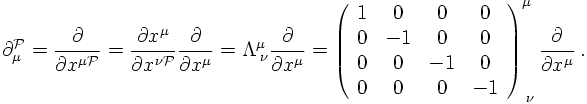Therefore, understanding Λ as a specific realisation of a general transformation acting on
the Dirac equation, the corresponding transformed solution ψ'(x') can be written as
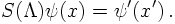In order to leave the Dirac equation invariant under this transformation, it must fulfil
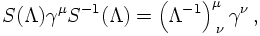where Λ is the transformation matrix. In the case considered here, it is easy to see that
the transformation S(Λ) must fulfil
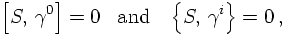leading to the identification
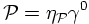with an arbitrary phase η. Fixing the phase and some simple calculations show that indeed
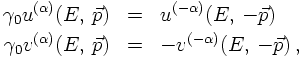implying that particles and anti-particles have opposite parity, where the sign is a matter of fixing
the phase, i.e. a matter of convention.