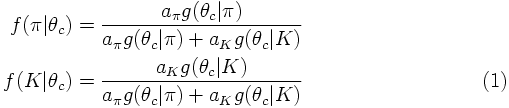Basics

Detector & statistics in a nutshell

1. Statistical data analysis in a nutshell
   
2. Probability
   
3. Probability Distributions
   
4. Cumulative Distributions
   
5. Expectation Values
   
6. Functions of random variables
   
7. Specific Probability Distributions
   
8. Parameter Estimation from Data
   
9. Statistical Tests
   In a statistical test one quantifies how well observed data agree with the probability of a given hypothesis which is usually called the 'Null hypothesis' H₀. Often the validity of the Null hypothesis is considered in comparison to 'alternative hypotheses' H₁, H₂, etc.
   
   Let's suppose that a set of data x=(x₁, ..., x_n) has been measured. Any function t(x) is called a 'test statistic' and is a random variable with p.d.f.'s g(t|H₀), g(t|H₁), etc. The statistical test is formulated as a decision to accept or reject a given Null hypothesis. For this purpose a 'significance level' α is defined which defines in turn the so-called 'critical region' t_cut by If the test statistic for the data x observed, t(x), is in the critical region the Null hypothesis is rejected. As a consequence, the probability to reject the Null hypothesis if H₀ is true is α. This is the probability for making the so-called 'error of the first kind'.
   
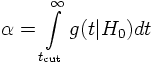
   Ex.: In a least squares fit the minimum χ² of the fit is a test statistic. If the observed significance level is considered being too small, or equivalently, the χ² value found is considered too large then one has doubts about the validity of one or more of the assumptions and rejects the fit (goodness-of-fit test). The significance level defining the critical region has of course to be chosen before the goodness-of-fit is made.
   
   If H₀ is accepted although it was wrong and another alternative hypothesis H₁ is correct one makes an error of the second kind. The probability for this error can be quoted if the alternative hypothesis is known and is given by:
   
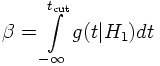
   Ex.: In a particle experiment the measurement of the Cerenkov angle θ_c allows to identify the nature of the particle if its momentum is known. The Cerenkov angle can be used as a test statistic. Let's assume that only two alternative hypotheses are to be considered: H₀=pion and H₁=kaon. One is then interested e.g. in a kaon selection with high efficiency and with a small misidentification probability for pions. For a given selection efficiency (1-α) the probability for pions to be misidentified as kaons is then fixed. For multi-dimensional test statistics this is not the case: for a given significance level (selection efficiency) the critical region can be optimized such that β becomes a minimum.
   
   The probabilities that a particle with an observed value of θ_C is a pion or a kaon depend on the relative frequency of pions (a_pion) and kaons (a_kaon), respectively, and are given by
10. Basic detector concepts
    
11. Problems