Detectors used in elementary particle and nuclear physics are based on the principle to transfer radiation energy to detector mass. Charged particles are transfering their energy through collisions to atomic electrons leading to excitation and ionisation. In most cases, neutral particles have to produce charged particles first inside the detector volume which in turn are transfering their energy by excitation or ionisation to the detector. All these interaction processes are random processes.
There is no detector which is perfectly suited for all possible applications. Depending on the application at hand detectors and complex detector systems are designed according to several criteria. There are several characteristics specifiying the features of a detector:
SENSITIVITY
The first question which arises is whether the detector is sensitive to the type of radiation and energy range under consideration. The detector sensitivity depends on the following factors:
* the interaction cross section with the detector material
* the detector mass
* the detector noise
* the protection material around the detector
Ex: If the interaction cross section is small (as e.g. for neutrinos scattering on a detector material) one needs a large detector mass in order to reach reasonable sensitivity if the incoming particle flux can not be significantly increased.
DETECTOR RESPONSE (FUNCTION)
Related to sensitivity is the detector response (function) to the radiation under study. Usually, the output signal of an electrical detector is a current pulse where the time integral of the signal corresponds to the amount of ionization produced by the particle-detector interaction. If the shape of the signal does not depend on the amount of ionization the amplitude of the signal is a measure for the radiation energy deposited in the detector. If this relation is linear the response of the detector is called to be linear.
It is possible that a particle of defined energy leads to a spectrum of signal amplitudes. This is called the detector response function. E.g. photons with definite energy may interact with the detector material by Compton scattering resulting into a broad spectrum of deposited energies due to the subsequent interaction of the recoil electrons. In contrast, charged particles with definite energies which are stopped within the detector material will rather lead to a Gaussian distribution of signal amplitudes.
ENERGY RESOLUTION
Suppose the detector is designed to measure the energy of a particle. Usually, due to fluctuations in the number of excitations and ionizations in the detector material, one observes a Gaussian-like peak for a monoenergetic particle beam instead of an ideal delta-function peak. The width of this peak determines the capability to distinguish particles with different energies. The energy resolution
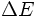
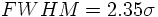
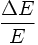
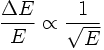
Example: We make use of the program identification which simulates the smearing of the measured energy in a electromagnetic calorimeter.
DETECTOR EFFICIENCY
The TOTAL EFFICIENCY of a detector is defined by the fraction of events registered at the detector with respect to the number of events emitted by a radiation source:
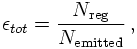
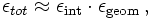
The geometrical acceptance depends in general on the polar and azimuthal angle of the emitted particle. It may depend also on the momentum of the particle (charged particles below a certain theshold momentum might be stopped due to energy loss before reaching the detector). The acceptance can also differ between different particle types: the detector device used to reconstruct charged particles may cover an angular range different from the detector device used to detect neutral particles.
In many cases, the intrinsic efficiency as well as the geometrical acceptance are determined by a Monte Carlo simulation.
RESPONSE TIME
This is the time between the arrival of the radiation and the formation of an output signal. If the signal is formed on a very short time scale with a fast rising flank a precise moment in time can be marked by the signal. This characteristics is of importance if timing information is crucial e.g. in Time-Of-Flight measurements with scintillators or in space determinations using a drift chamber through drift time measurements.
The duration of the signal is also important if dead time or a pile up of subsequent signals may become important as discussed in the next subsection.
DEAD TIME
Related to efficiency is the dead time of a detector. The process of energy (charge) deposition and the 'readout' of the information takes a finite time in which the detector and its associated electronics is not able to register a subsequent signal. Depending on the type of detector and the rate of particle interactions with the detector material the issue of dead time can be rather important.
If the detector is insensitive to other events during the 'readout' time these events are lost. If the detector is sensitive to additional events during the 'readout' time these events may pile-up resulting in a distortion of the signal.
In experiments with large particle fluxes dead time can be reduced by designing the detector with a high granularity such that the occupancy per detector cell is reasonably small. The occupancy measures the number of particles traversing a detector cell per event. This will however increase the costs of building the detector and its readout electronics.
Pile-up can be reduced by shaping the detector signal such that a very short and as a consequence a small signal is formed. This however is limited by the inherent noise of the detector.