In classical electrodynamics, the electric and magnetic field strengths are considered as the basic quantities whereas the four-potential is introduced as a convenient mathematical object. Since the four-potential is not uniquely determined due to the freedom of a gauge transformation it does not seem to have physical significance.
In quantum mechanics and quantum field theory however this is definitely not the case as it has been pointed out by Aharanov and Bohm and as we have seen just beforehand:
the electromagnetic four-potential Aμ induces a phase transformation of the Dirac field of a charged particle which can be observed (AHARANOV-BOHM effect) and has been experimentally realized by Chambers!
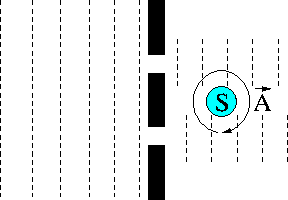
An electron beam is split into two coherent beams and are let to interfere resulting in an interference pattern. A solenoid S is placed after the beam split. The magnetic field is only present inside the solenoid but not outside. However, outside the solenoid a vector potential is present. The strength of the vector potential can be changed by altering the current inside the solenoid.
The vector potential produces a magentic flux and consequently produces a phase change of the electron wave function which is different for the electron beams passing the solenoid on the left and on the right side. As a consequence, the relative phase between both electron beams is changed by the vector potential resulting in a shift of the interference pattern. This has been experimentally verfied by Chambers.