QED

Gauge Invariance

  1. Gauge Invariance in Classical Electrodynamics
  2. Phase invariance of the Dirac field

    GLOBAL PHASE INVARIANCE
    In the following the Lagrangian of a free Dirac field describing a particle with mass m is considered:
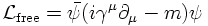
    freediraclagrangian
    It is possible to change the absolute phase of the Dirac field without changing the physics, i.e. the Lagrangian is invariant under the transformation
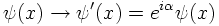
    globalphasetrafo
    Also the E.o.M., that is the Dirac equation, is invariant under such a transformation:
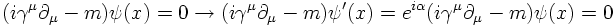
    eomglobalphasetrafo


    LOCAL PHASE INVARIANCE
    What happens if one chooses a different phase at a different time-space coordinate?
    The field is changed then by
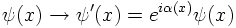
    localphasetrafo
    and the derivative in the Dirac equation becomes
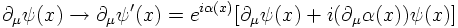
    derivativelocalphasetrafo
    As a consequence, the last term spoils the invariance under a local phase transformation.
    Local phase invariance can be achieved however by the following replacement:
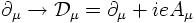
    covariantderivative
    where e is the charge of the particle described by the field ψ and the new field Aμ transforms under the phase transformation as
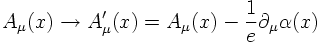
    fieldlocalphasetrafo
    which looks like a gauge transformation of the electromagnetic four-potential.
    Hence, one has to pay a price in order to achieve local phase invariance. A price however which is very welcome: Local phase invariance is not possible for a free particle field but one needs to introduce an additional field which couples to the particle via the (electric) charge as the electromagnetic field does.
    This is an example how a fundamental interaction (here electrodynamics) can be introduced by the dynamical principle of LOCAL PHASE INVARIANCE or LOCAL GAUGE INVARIANCE!

    GAUGE INVARIANCE IN QUANTUM MECHANICS
    One could have chosen another point of view and started with the equation describing a Dirac particle with charge -e interacting with an external electromagnetic four-potential. In this case the Dirac equation reads with the generalized momentum pμ + e Aμ:
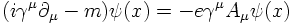
    diracequationwithemfield
    One can then change the four-potential applying a gauge transformation:
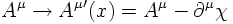
    gaugetrafo
    The Dirac equation is only consistent with electrodynamics, that is, invariant under such a gauge transformation, if the Dirac field is simultaneously changed by a local phase transformation:
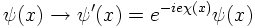
    correspondinglocalphasetrafo


    (NON-)ABELIAN GAUGE GROUPS

    The local phase transformations discussed so far are forming a group: U(1).
    As a consequence, the order of two subsequent local phase transformations does not matter, that is, they commutate. Hence, QED is said to be an ABELIAN LOCAL GAUGE THEORY.
    Weak interations and QCD are examples of NON-ABELIAN GAUGE THEORIES. The main consequence of non-commutating local phase transformations is the fact that the gauge fields (W,Z and gluons, respectively) are carrying charges themselves resulting in self-interactions of the gauge fields.

  3. The Aharanov-Bohm effect