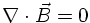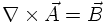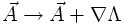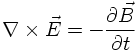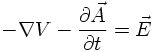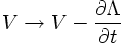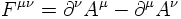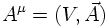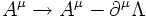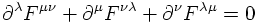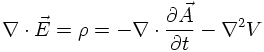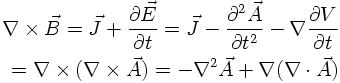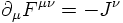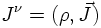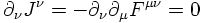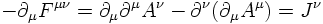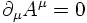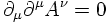QED
Gauge Invariance
- Gauge Invariance in Classical Electrodynamics
Maxwell's equation
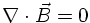suggests that there is a vector potential fulfilling
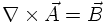The magnetic field is unchanged if one adds a gradient of an arbitrary scalar field Λ:
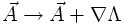Similar in line, the Maxwell equation
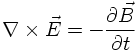suggests that there is a scalar potential V fulfilling
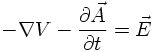In this case one can add a time derivative of an arbitrary scalar field Λ
to the scalar potential V
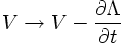without changing the electric field.
To summarize this in a covariant notation: The field-strength tensor
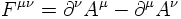with
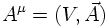is unchanged under a 'gauge transformation'
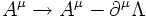with Λ(x) being an arbitrary function.
The same electrodynamics can be described by many different four-vector potentials.
This is what is meant by GAUGE INVARIANCE of classical electrodynamics.
The two Maxwell equations from above are then rewritten as
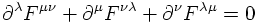The two remaining Maxwell equations
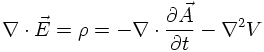and
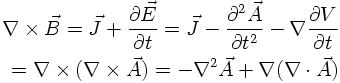can be written in the compact form
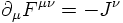with the electromagnetic current being
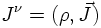
CONSEQUENCES
1) The electromagnetic current is conserved:
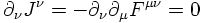2) The time derivative of the electric field in the fourth Maxwell equation
guaranteeing local charge conservation leads also to the prediction of
electromagnetic waves:
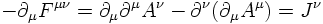In the absence of external electromagnetic currents and using the Lorentz gauge
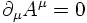one obtains for each compoenent of the four-potential (identified with the
photon field) a Klein-Gordon equation for a massless particle:
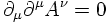
- Phase invariance of the Dirac field
- The Aharanov-Bohm effect