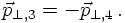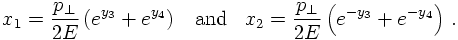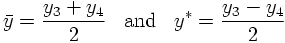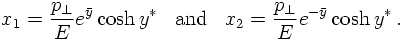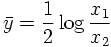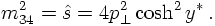VARYING CENTRE-OF MASS ENERGIES
As already mentioned above, there are situations when the energies of the particles in the initial state are not fixed which trigger the reaction. In particular, this is true for experiments with colliding hadrons, such as protons. When these hadrons are "prepared" in the accelerator, their respective energies are pretty much fixed; in most cases, the energy-smearing due to machine effects is completely negligible, and the energies can to an excellent approximation be considered as the same for all particles in a beam. However, hadrons have a substructure, they consist of constituents, usually denoted as partons. These constituents can be thought of as the quarks and gluons forming the hadron in question. Their individual four-momenta add up to yield the four-momentum of their parent hadron. The binding energy of the partons can be though of as being of the order of the hadron mass, roughly 1 GeV. In fact, this is a consequence of the structure of strong interactions, which will be discussed in a later chapter. If, however, a reaction occurs with characteristic energy scales much larger than the binding energy, the partons inside the hadron are resolved - in other words, it is them, who interact individually, rather than the collective interaction of all partons inside a hadron. To describe this, a few assumptions can be made, which will turn out later, to be valid to a good approximation:- partons are massless;
- they move in parallel with their parent hadron, i.e. taking the beam to be parallel to the z-axis translates into the partonic four-momentum having neither an x- nor a y-component;
- their energy fraction w.r.t. the hadron energy is described by a quantity called
the Bjorken-x (a refinement of this will be presented later), summing it over all
partons inside a hadron yields one,
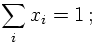
- the probability of finding a parton of a certain kind inside a given hadron is determined through a function of the Bjorken-x and the characteristic resolution scale of the partons inside a hadron, f(x,Q). It is called a parton distribution function. This function is universal for the hadron and parton species and in that sense, process-independent.
At this point it should at least be noted that also for point-like incoming particles, such as electrons, whose energy in principle is fixed, a similar reasoning can apply. This is because charged particles are usually accompanied with a coherent cloud of virtual photons, which, as a consequence of quantum mechanics, are produced, exist for some limited time and recombine with the electron. When an interaction occurs this coherence is broken, and the electron interacts with duly reduced energy. Of course, using the same Bjorken-x idea of above, the probability of finding an electron-"parton" inside an electron peaks at x=1. Again, this will be discussed later.
In both cases, in order to calculate a cross section, the partonic initial state is not fixed any longer, implying that an integral over all configurations has to be performed. Usually this translates into the following
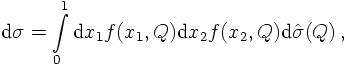
CONNECTING THE BJORKEN-X WITH S AND Y
However, at this point it is worthwhile to consider the effects of this intrinsic structure of the beam particles on kinematics. According to the assumptions above, and taking all partons to be massless, their momenta can be written as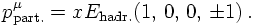
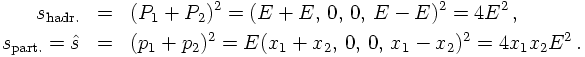
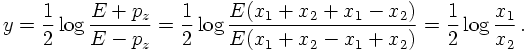
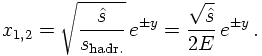
SPECIFYING FOR 2→2 PROCESSES
Often, the scattering processes in question are of the type 2→ 2, see above for details. Assuming the hadronic c.m. system to be the laboratory system, the tranverse momenta of the outgoing particles just compensate each other, i.e., in two dimensions,