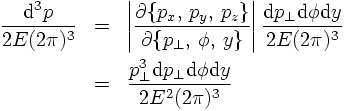Basics

Simple relativistic kinematics

1. Four-momentum conservation
   
2. Orientation with respect to the beam axis
   

   THE BEAM AXIS IS SPECIAL

   In most cases, there is a special axis defined through the geometry of particle physics experiments, namely the beam axis - the axis parallel to the incoming beams. In most experiments (BaBar is a famous exception), this axis is uniquely defined. Even in BaBar, where the beams cross under an angle in the laboratory system, a boost (Lorentz-transformation) can be applied, to find a system, where the beams collide "head-on". However, usually, this beam axis is chosen to be the z-axis. In most cases, the position, where the beams are brought to collision, is pretty well-known; this knowledge is used to fix an "origin" of the coordinate system. As long as the incoming beams are not polarised, there is thus only one particular axis, and in such cases, events exhibit cylindrical symmetry w.r.t. the z-axis.
   Therefore, it is often convenient to describe four momenta of particles by their energy (yielding the absolute value of the three-momentum through the on-shell condition p² = m²), and by two angles θ and φ. Here the "polar" angle θ describes the angle of a particle w.r.t. the z-axis, and φ is the "azimuthal" angle around the beam axis.
   
   

   RAPIDITY AND PSEUDO-RAPIDITY

   Instead of using the polar angle θ it is sometimes more useful to have a quantity with better properties under boosts along the beam axis. This is especially true for experiments with colliding hadrons, since usually only some constituents of them interact. In such cases, the energies and therefore the momenta of the incoming hadrons are known, but the energies and momentum fractions of the respective constituents that interact are not known a priori. Assuming that the constituents move in parallel to the incoming particles, this implies that the overall momentum of the colliding constituents along the beam axis is essentially unknown. One could then characterise their collision by the relative motion of their centre-of mass system in the lab system and by their centre-of mass energy. The relative motion can be understood as a boost of the constituent system with respect to the lab or beam system. It is thus convenient to construct a quantity with good transformation properties under boosts along the beam axis. Such a quantity is the rapidity, usually denoted by y. 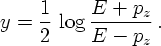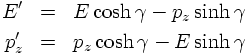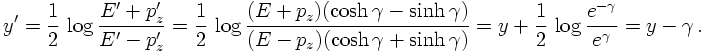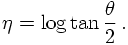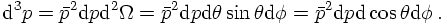It is defined as It is simple to show that rapidity differences remain invariant under boosts along the z-axis. To do so, it is enough to prove that rapidities change additively under boosts. Any boost is parametrised by a boost parameter γ and by defining an axis. Energy and three-momentum along this axis (here for obvious reasons the z-axis) then change according to Hence Unfortunately the rapidity does not provide a very intuitive interpretation. Therefore, another quantity has been introduced, called the pseudo-rapidity, which is commonly denoted by η. Employing the polar angle θ, it is defined through The location of individual varying momenta can be seen in this graphical display. These momenta are distributed uniformly in their solid angle, i.e. according to Obviously, a uniform distribution of momenta with fixed length translates into a distribution that is uniform in φ and in cos θ. Uniform distributions of momenta in terms of polar coordinates, pseudorapidity, etc.. are shown in this graphical display.
   For massless particles, rapidity and pseudo-rapidity are identical. This can be seen from where the fact has been used that for massless particles In contrast, for massive particles, pseudo-rapidity and rapidity do not conincide. This can be seen quite easily: From its geometric definition through the polar angle θ, it should be clear that pseudorapidities range from minus to plus infinity. Rapidities, however, are constrained by Similar reasoning yields the minimal rapidity - of course, the corresponding range is symmetric.
   
   

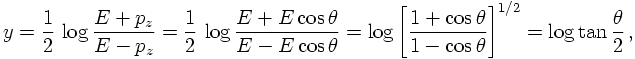
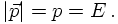
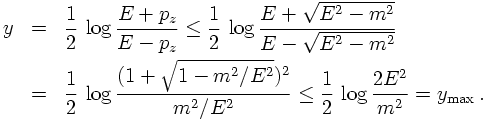
   TRANSVERSE MOMENTUM AND SUCH

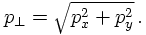
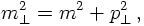
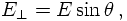
   Since rapidity (or, similarly, pseudo-rapidity) entangles energies and longitudinal momentum, it is useful to have other, independent quantitites that characterise momenta in collider experiments. For symmetry reasons, the azimuthal angle φ is usually employed; in addition it has become customary to also use transverse momentum, defined by There are a number of similar quantities around, all of them stressing the transverse event plane, which also is invariant under boosts. This invariance is not fully satisfied in all of the following quantities, though. First of all, also a transverse mass can be defined as which is clearly invariant under longitudinal boosts. In contrast, a transverse energy can be defined as the geometrical projection of the energy on its "transverse" component, which doesn't need to be longitudinally boost invariant.
   Of course, there are plenty of situation where it is an advantage to reformulate the integral over a particle's momentum in terms of rapidities and transverse momenta.
   
   
3. Mandelstam variables
   
4. Hadronic collisions
   
5. Problems