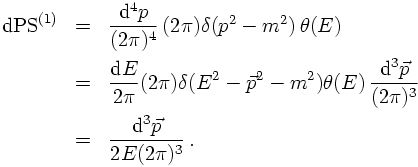Basics

Simple relativistic kinematics

  1. Four-momentum conservation

    UNITS AND FOUR VECTORS

    Before going into much detail about kinematics, it is important to remember a number of basic identities. First of all, it must be clear that in particle physics most things move with large velocities - in other words with a considerable fraction of the speed of light. Since particle physics also is the world of quantum physics, it is common to set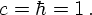
    c=h=1
    This allows to write four-vectors without any disturbing c's or Planck's constants as
    Four-vectors have to satisfy the following on-shell relation
    where, as above E is the energy, the pi are the components of the three-momentum, and m is the mass of the particle in question.

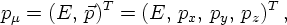
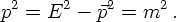
    FOUR MOMENTUM CONSERVATION: EXAMPLE

    Of course, in physical processes, both energy and momentum must be conserved. This can easily be interpreted in a relativistically invariant fashion as four-momentum conservation. In particular, if, for instance, a particle with four-momentum p decays into two particles with four-momenta q and r, respectively, a(p) → b(q) + c(r), the momenta must satisfy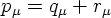
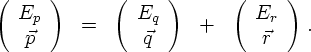
    or, in components
    From this, it is clear that in the centre-of mass frame of the decaying particle p the spatial components of the outgoing momenta r and q must balance each other. Also, for massless q and r it is obvious that both particles have the same amount of energy in the very same frame, namely half the (virtual) mass of the decaying particle. The relative amounts of energy are shifted if the two outgoing particles acquire different masses.
    The determination of the exact energies of the two particles q and r in the rest frame of the decaying particle p is left as an exercise.
    In order to integrate over four-momenta, as needed in the calculation of cross sections from the S-matrix (see above), a corresponding covariant volume element dP in momentum space needs to be introduced. Apart from the integration measure and some factors of 2π, there are two more ingredients, namely a δ-function incorporating the on-shell condition, and the requirement that all physical particle energies are positive. Taking together, this yields


  2. Orientation with respect to the beam axis
  3. Mandelstam variables
  4. Hadronic collisions
  5. Problems