Basics

Simple kinematics

  1. Relativistic kinematics and four-momentum conservation
  2. Orientation with respect to an axis (the beam axis)
  3. Mandelstam variables
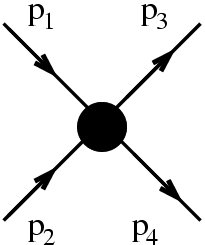
    It is clear that physical scattering amplitudes should better be independent of the frame they're calculated or measured in. This translates into the fact that they depend on covariant quantities only: Masses (or, better, their squares) and products of four-momenta. Basic scattering or production processes at collider experiments are typically of the form 2→ 2:
    where a, b, c, and d label different particles and the various p label their respective momenta. This leaves three independent scalar products of pairs of momenta, namely
    The last identifications in each line are valid for massless particles in their centre-of mass frame only. In this frame, θ is the scattering angle, i.e.\ the angle between the momenta of particles a and c. For both massless and massive momenta, the Mandelstam variables satisfy
    which is obviously true for massless particles. This identity implies that only two of three of these variables can be chosen at will. Usually, the choice is made to fix s, the squared centre-of mass energy of the produced (in general: final state) particle pair, and to fix t, the momentum transfer. From the identiy above, also
    follows. Consider now the following diagrams, where the thick black blob of the process scetch above has been decoded.
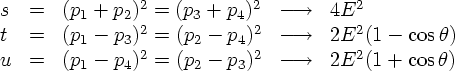
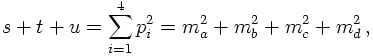
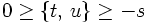
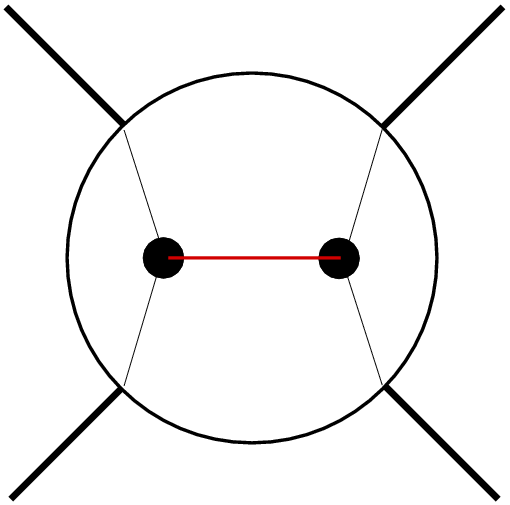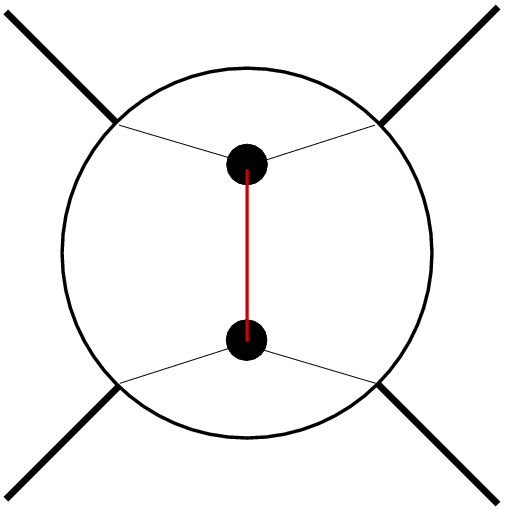    s-channel process:
    the scattering process is realised through the exchange of a virtual particle with momentum p=p1+p2     		t-channel process:
    the scattering process is realised through the exchange of a virtual particle with momentum p=p1-p3
    Of course, real processes may be more complicated, for instance, by mixing two or more different ways in which they can proceed. In such a case, the total quantum mechanical transition amplitude can be represented as the sum of individual contributions, i.e., as a sum of their respective amplitudes. However, it is clear that specific processes may be dominated by amplitudes like the left one in the figure above. In such a case, the diagram is usually coined an "s-channel" diagram with corresponding "s-channel kinematics". Later on, this will be discussed in more detail.

  4. Hadronic collisions
  5. Problems