QCD

Multiple gluon/parton radiation

1. e⁺e^-→ hadrons at higher orders
   
2. Jets
   

   WHY JETS

   In the previous section the emission of an extra gluon in electron-positron annihilation into a quark-antiquark pair has been discussed. It was found that the differential cross section exhibits a singularity, if the gluon energy or its angle w.r.t. either the quark or the antiquark approach zero. Of course, the question whether this is a relevant singularity, depends on the experimental ability to resolve this gluon. In addition to this individual gluon emission, and in view of the discussion of the singularity structure in multiple emission processes leading to a jetty structure of QCD events it seems natural to provide a definition of what a jet is. In fact, this definition will also provide some criteria describing the resolution of QCD radiation. Anyways, before going into any detail there, it is worth to view a few typical QCD events to gain some feeling for how to define jets at all.
   • Jets in ee→ hadrons at LEP (pictures from CERN database)

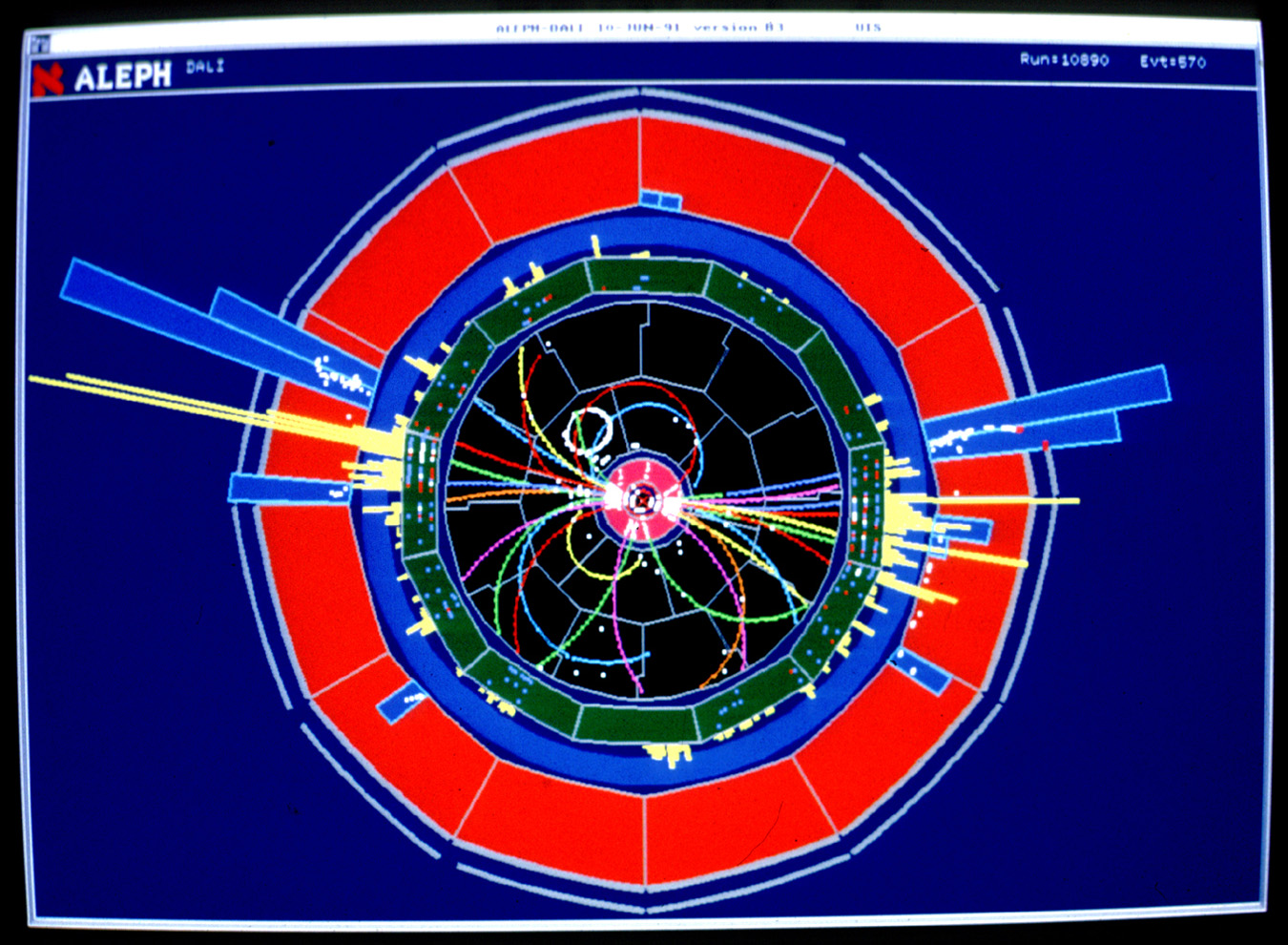
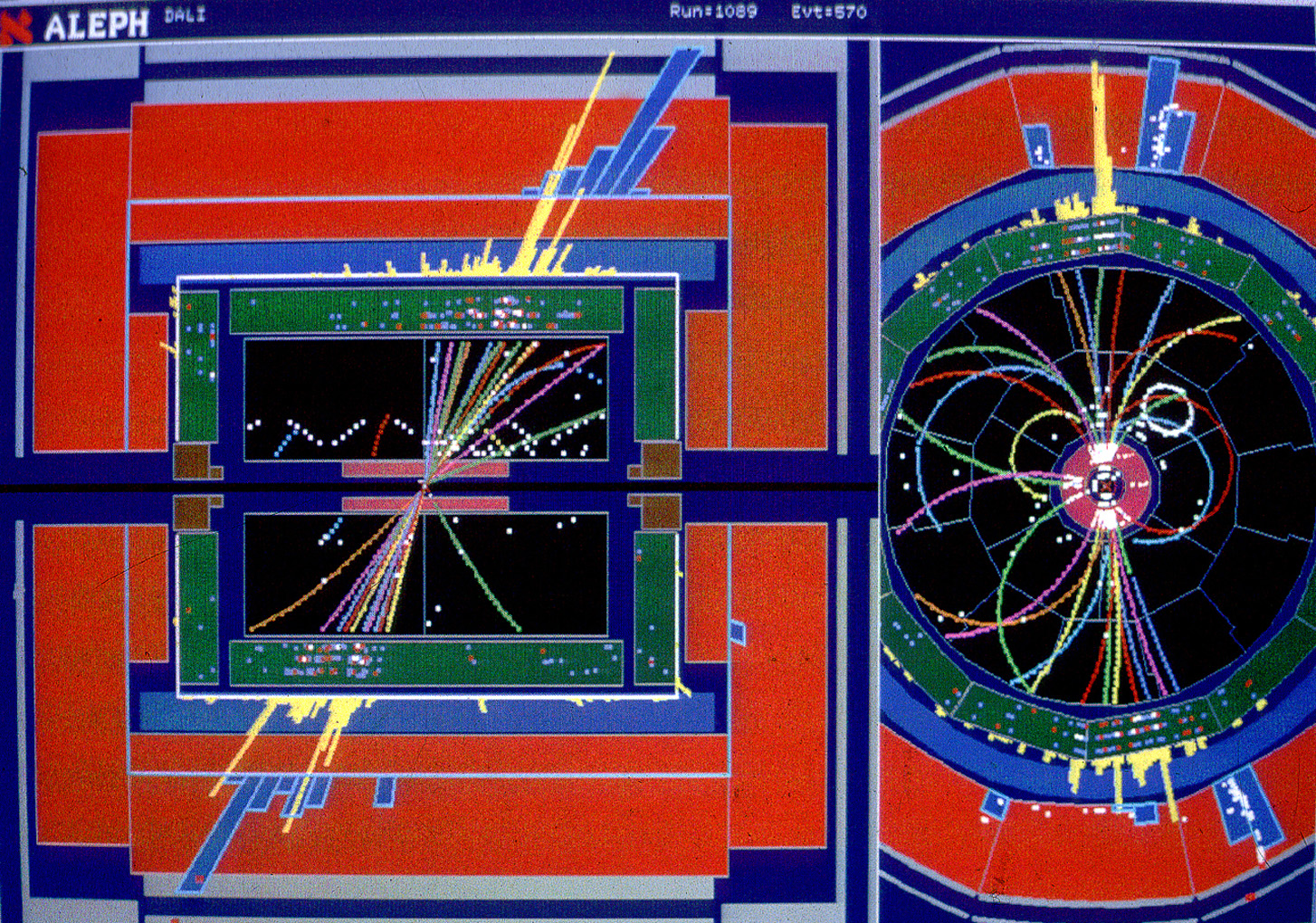
     Jets at the Z-pole (Aleph, LEP1)	Jets at the Z-pole (Aleph, LEP1)
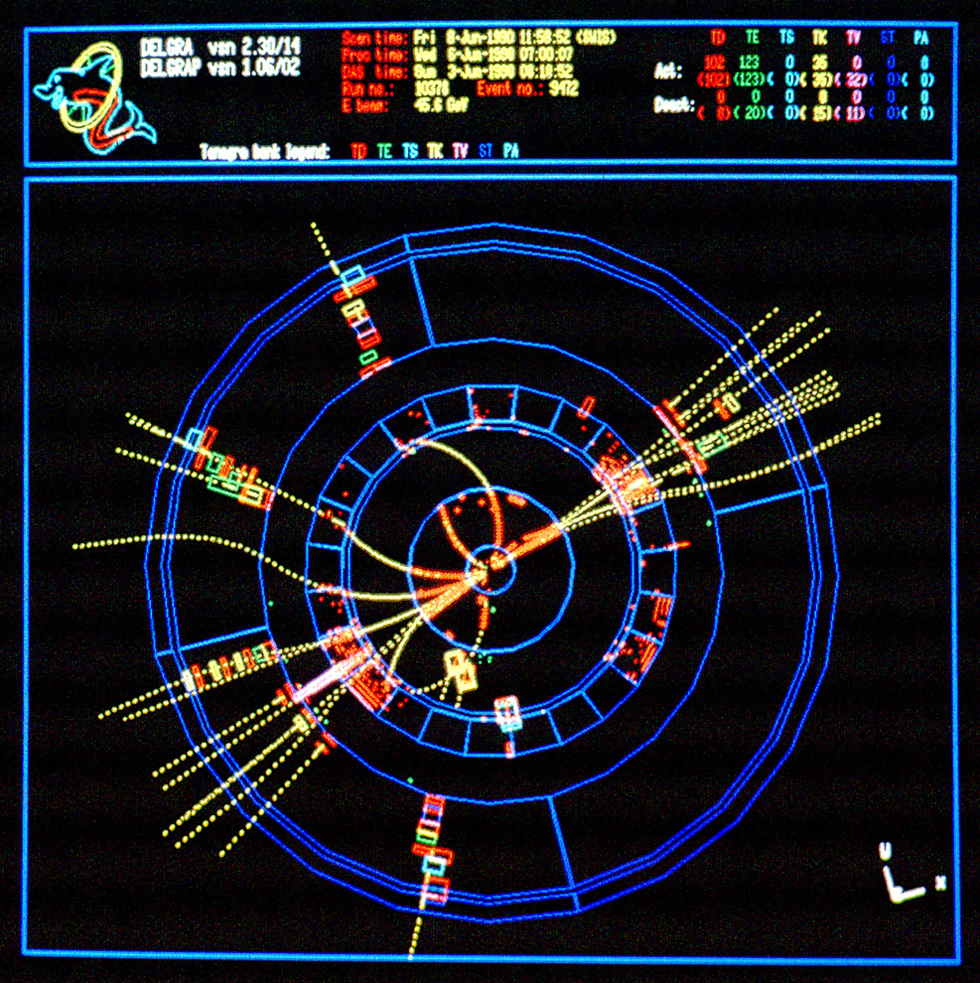
     Jets at the Z-pole (Delphi, LEP1)	Jets at the Z-pole (Delphi, LEP1)

     
     
     
   • Jets in pp collisions: 2 jets, E_T = 616, 557 GeV (pictures from D0, Tevatron)
     
     
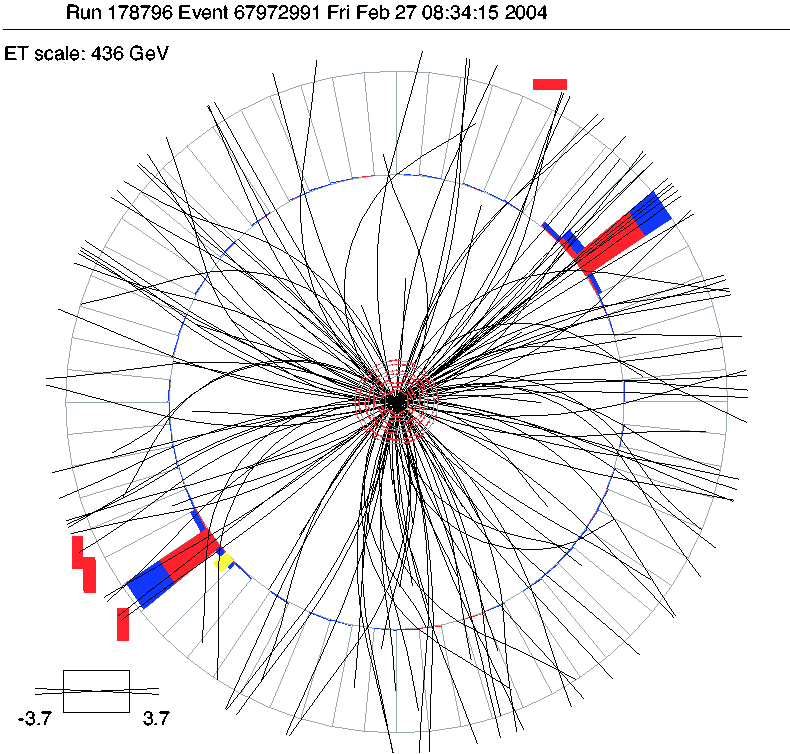
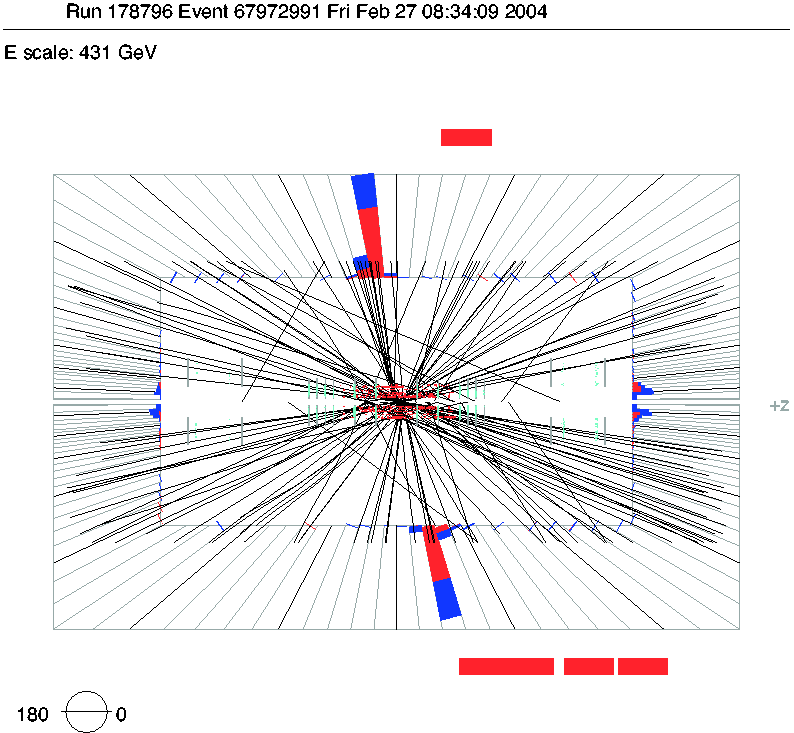
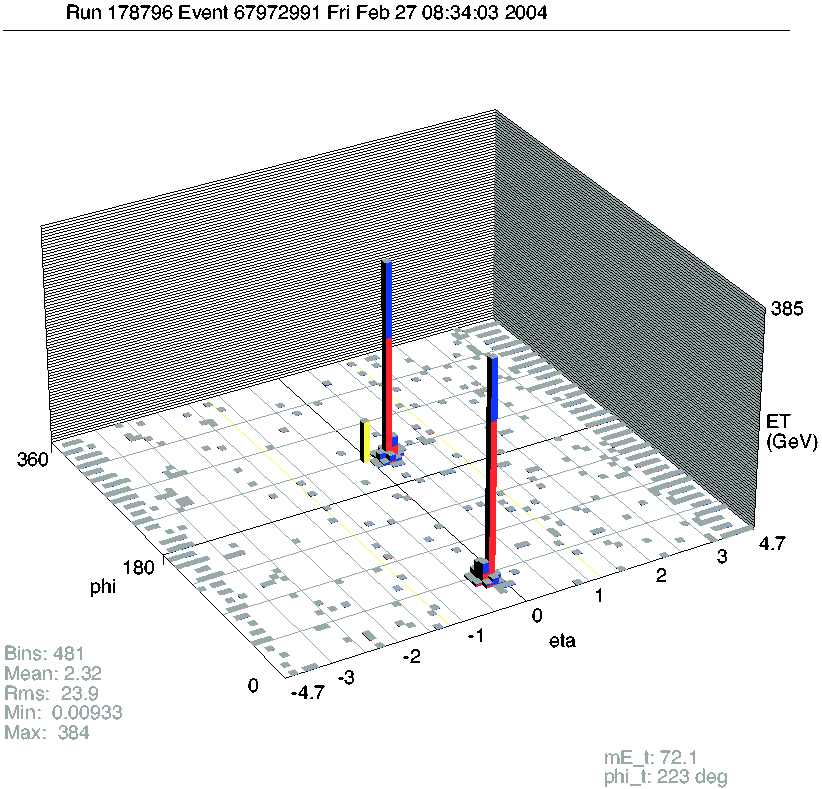
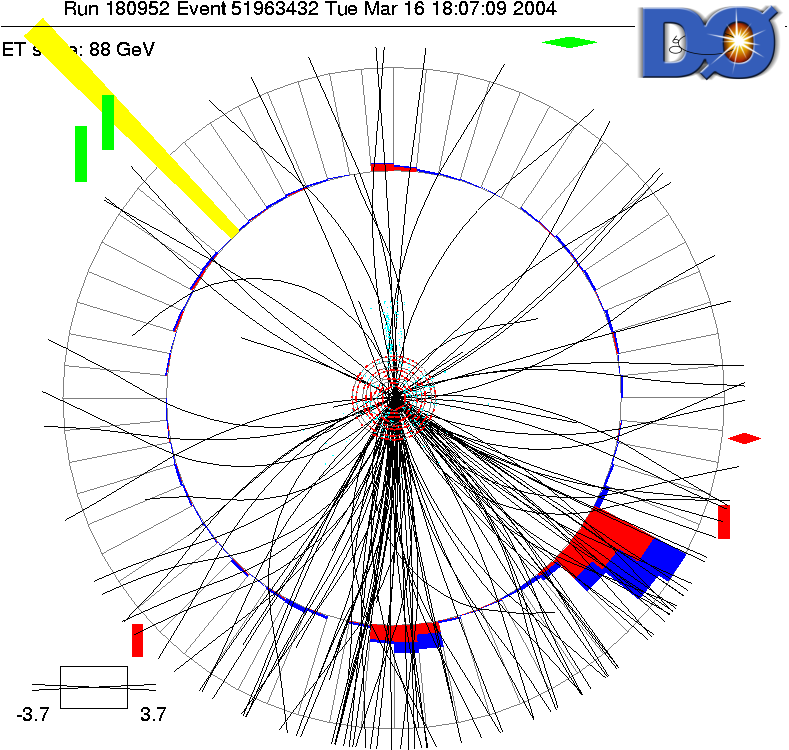
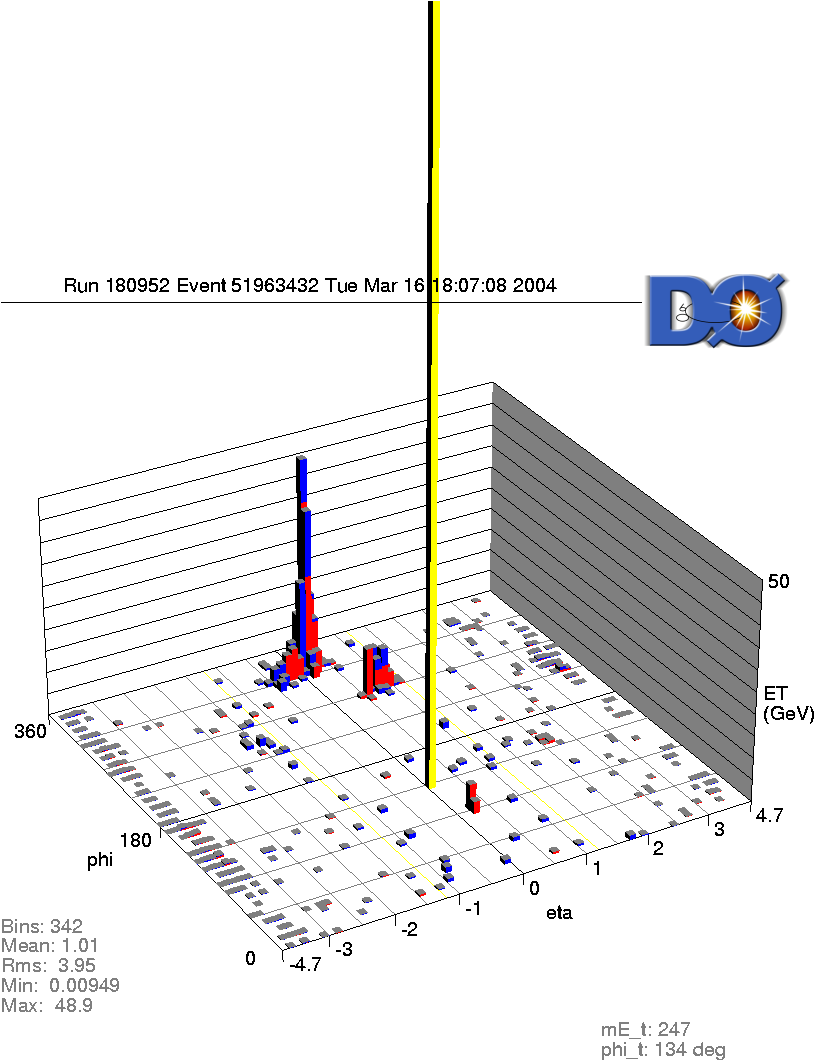
   • Jets in pp collisions: 4 jets, E_T = 289, 117, 14, 11 GeV + missing transverse energy, E_T = 381 GeV (pictures from D0, Tevatron)
   
   
   

   JET DEFINTIONS

   After viewing these event displays the question arise naturally how to quantify such clusters of hadronic energy. This is usually down in an iterative fashion. In the following, two algorithmical ways of defining jets will be discussed:
   • "Geometric definitions"
     The idea here is to find regions in the detector where hadronic energy collimates, and to call this a jet. There are different algorithms for this, on very different levels of sophistication, here only the simplemost of these "cone" algorithms will be presented:
     1. Check all entries in your calorimeter and select the one with the largest energy deposit.
     2. Draw a "cone" around this entry with a given radius (this translates into cells in the η-φ plane) to add up all entries.
     3. Construct a summed four-vector from these entries by projection of energy and direction of the normal vector of the cell.
     4. If the eenrgy of the resulting vector is larger than a given value, the object is a jet. Then the cells beloning to this jet cannot be used again. If no jet emerges continue with the next largest energy deposit.
     5. Repeat this exercise, until no more jets are found.
     Clearly, the parameters of this algorithm are the cone-radius R and the threshold energy E for jets.
   • "Clustering" of particles/detector cells
     The idea here is to go over all particles or detector cells, in the following called "entries" and clustering pair-wise the "closest" two into a new entry, where distance is defined according to some measure, until all entries are disjoint jets. The algortihm for this in more detail reads as follows:
     1. Check all pairs of entries i and j and calculate their relative distance d_ij, given by in the case of ee annihilations or by in hadronic interactions, where D is a parameter of the algorithm and usually smaller than one. In hadronic interactions, outgoing hadronic matter can also be clusterd with an incoming hadron, in this case the distance reads
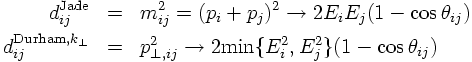
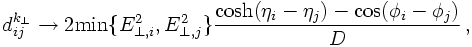
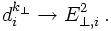
     2. Cluster those two entries i and j in the final state or, eventually, just i with an initial state particle, that have the smallest distance. The resulting particle inherits the summed momentum of the two clustered particles. For this addition of momenta of two particles clustered into one particle one may either demand that all momenta are taken as massless or not; in the former case, these is clearly a contradiction in the addition of two light-like momenta and demanding that the result is also light-like. To cure this, either the energy or the three-momentum has to be fixed, the other one has to be adjusted. This then is called either E or P-scheme.
     3. Repeat this exercise, until any possible pairing has a distance larger than a predefined "jet-measure". The remaining entries are the jets.
     
     
     

     HOW THIS HELPS

     The definitions above provide a cut way of cutting away "dangerous" regions - soft and collinear - of differential cross sections for extra parton emission. The idea, at least at leading order, is to just demand that all partons produce a jet :this will regularise all tree-level QCD amplitudes. Equipped with such a defition, one may now try to calculate the three-jet cross section at leading (possible) order in QCD in the, say, Jade algorithm. To do so, the Jade definition of the distance d must be translated into cuts on the two x in the differential cross section. 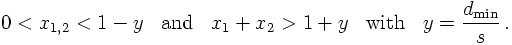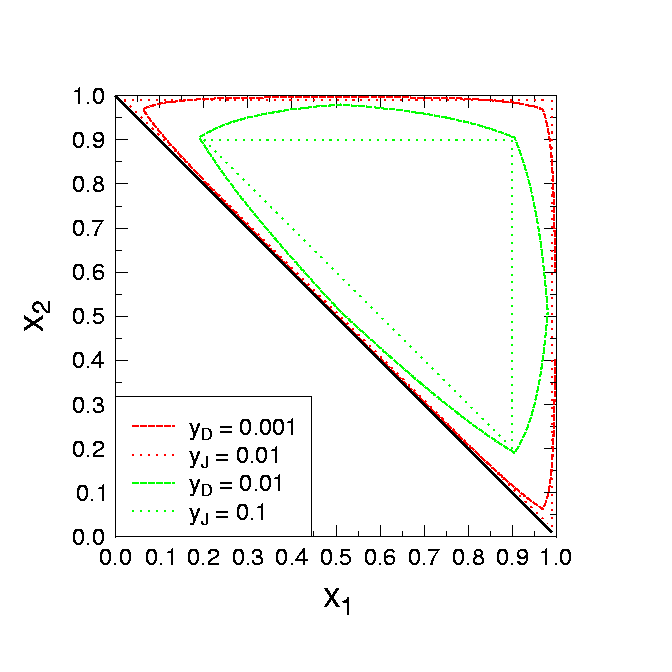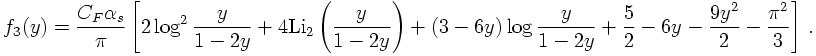After some algebra, one finds that These bounds, and also, similarly, for the Durham algorithm, are depicted below. For the Jade algorithm the three-jet rate, the fraction of three-jet events in the total cross section, reads The Li-function here is the dilogarithm, a function notorious in higher order calculations. For y→ 0 is approaches 0.
     For y→ 0, clearly a double-logarithmic structure emerges, yielding a three-jet rate larger than one for small values of y, clearly an unphysical result, which would be cured only, if even higher orders were included. Anyways, at this point it should be clear that consequently at this order in the strong coupling constant the two-jet rate is just 1 minus the three-jet rate.
     Some comment is in order here: As it turns out, the Jade algorithm is not perfectly "infrared safe"; cuts defined though the invariant mass only poorly reflect the radiation pattern of QCD. Therefore, in most modern ee experiments, the Durham- or k-perp-algorithm has been chosen. This class of clustering algorithms has much nicer properties; in fact, jets defined through them lead to jet rates that can be resummed. But before looking into this feature, let us anylse in a bit more detail the logarithmic behaviour of parton emission, which will lead to the splitting functions needed for a proper resummation.
     
     
   • Large logarithms and splitting functions
     
   • Resummation/exponentiation
     
   • DIS: Deep inelastic scattering and the DGLAP evolution equation
     
   • Drell-Yan processes at hadron colliders