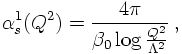In the previous section some phenomenological models for the quark-antiquark potential in the static limit have been discussed. The natural question arises how this behaviour of the interaction strength, large at large distances and small at small distances, can be understood from first principles, i.e. starting from the Lagrangian. A simple way to look at it is to consider higher-order corrections to fermion-fermion scattering: in QED this would be electron-electron scattering, in QCD quark-quark scattering is a good candidate. At first order in the perturbation theory closed loops appear inside the photon/gluon propagator, respectively (Test question: which ones?). When inspecting them it becomes apparent that they diverge as the momentum running inside the loop goes to infinity. This effect is called ultraviolet divergence. In quantum field theory, this is dealt with by regularising the divergencies and by construction of appropriate ultraviolet counter terms that are added to the original Lagrangian and render it ultraviolet finite. However, these counter terms induce some freedom to the theory, since finite pieces may be treated in different ways. As a consequence, renormalised, i.e. physical, quantities, such as coupling constanrts must be measured in order to fix them at one point, where they have been measured. If then this quantity is used at a different scale, the renormalisation procedure induces a change of the quantity, which thus runs.
In QED, at first order, the coupling constant is usually fixed in the Thomson limit, i.e. for static poles at large distances. Thus the reference is
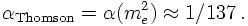
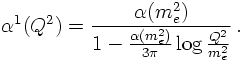
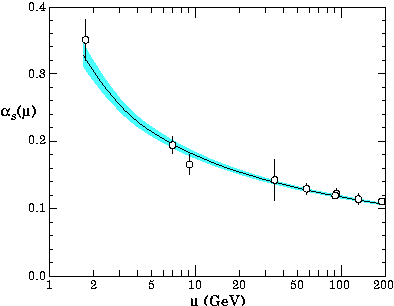
In QCD the behavior of the coupling constant is strikingly different. There,
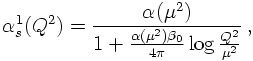
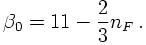
That's why other reference scales are needed in order to fix the coupling constant, once its scaling behaviour is known. At this point it is important to note that it does not matter which point μ is chosen as a reference point; at any given order of the calculation, the difference between two different choices is at higher orders. This allows to systematically reduce the dependence on the scale choices in any calculation. In turn, suitable scale choices in a caluclation can be used in order to minimize the dependence of higher order terms on the actual result.
Another point is worth discussing here: Due to the freedom in choosing a reference scale for the coupling constant one may try to introduce a "real" parameter Λ in terms of which the coupling constant can be calculated: