QCD

Asymptotic freedom

1. The effect of hadrons as bound states of quarks (and gluons?)
   It is a fact that no free quark or gluon can be observed in any detector, instead the quanta of QCD always appear as the constituents of bound states, the hadrons. This is due to the fact that the strong coupling constant α is strong - and that it becomes stronger with increasing distances. Pictorially speaking, the force on colour charges, induced by the strong interaction behaves quite similar to the one of a harmonic oscillator. In fact, there is a large class of phenomenological models for hadron wave functions that are based on a potential for the strong interaction; they all have in common that the potential rises linearly with the distance, like V(r) = κ r. (Usually, to model also the small distance behaviour, a Coulomb-like interaction, propotional to 1/r, is added.) It is amzing how well such a simple ansatz is capable of describung cross features of hadrons, like, e.g. mass eigenstates, especially in heavy quarkonia. In turn, such models immediately imply that an infinite amount of energy is needed in order to separate a quark or any coloured object, from a hadron. As a consequence, any separation that is large enough will lead to the spontaneous creation of a new colour-anticolour pair in the colour field, similar to the spontaneous creation of electron-positron pairs in strong electromagnetic fields. This latter process is known as the Schwinger mechanism, described in a truly non-pertubative way. There, the production probability for a pair to be created in a homogenous electric field is given by P = exp(-πm²/σ), where σ is the "string-tension" of the electric field given as a function of the field strength.
   When going beyond simple phenomenological models and trying to include the underlying structure of the theory, approximations must be made. One of them is the simple assumption (which, however, is valid for heavy quarkonia) of having static colour sources in a triplet-antitriplet state, which can be easily identified as a quark-antiquark state with infinite quark masses. In such an approximation there is only gluons left that drive the interaction. To gain a gauge invariant form of the potential therefore the gluon fields have to be arranged in a guage invariant quantity. Such a quantity is the quantum mechanical expectation value W(P) of the Wilson loop, given by the expectation value of a heavy quark-antiquark pair from x to y along a path P, Since the colur charge of the antiquark is opposite w.r.t. the quark, the line integral is along a closed line (going from x to y for the quark and from y to x for the antiquark), which can be transformed such that a closed loop with an included minimal area can be defined. The trace in the expression above reflects the fact that we're talking a bound state, i.e. a colour singlet and that an average over all allowed configurations is taken. Anyways, it is important to note that this quantity is gauge invariant. It can be shown that this expectation value scales like the exponent of the minimal area included by the path, which implies that V(r) = κ r for large r.
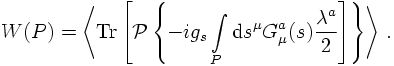
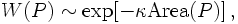
   The appearance of the exponent signals that this Wilson loop takes into account also non-perturbative effects, describing confinement. Ideas to interpret this stem from the theory of superconduction, and they are known as chromoelectrical Meissner effect.
   These ideas can be incorporated in a model fro the linear potential known as the Nielsen-Olesen string. The idea is that the field between the individual monopoles is "squeezed" into a thin tube, which, asymptotically, has vanishing diameter. In other words, the gluonic field between the quark and the antiquark can be described by a string. This string has a constant field energy per unit length, like in the linear potential.
   
   This confinement of the quarks and gluons has some far-reaching consequences when it comes to testing the theory:
   • For high energies/small distances the potential behaves like a Coulomb potential: QCD can be described by perturbation theory like QED (only more complicated due to the non-Abelian structure of the theory). For small energies/long distances the confining term wins and bound states emerge. In most cases bound states cannot be describe by the methods of perturbation theory, consequently pertubative QCD fails almost always in these regiions.
   • Any direct measurement of genuine QCD quantities such as the coupling constant between quarks and gluons is indirect and "spoiled" by bound state effects. These can in most cases not be cacluclated from first principles.
   • As a consequence, there is a need for "infrared-safe" quantities; such quantitites that do not rely on specific hadron properties or on the details of the transition from free quanta to bound states.
   • In most cases the hadron wave functions described above a good only for static properties of the hadrons. Quantum fluctuations like, e.g. creation and annihilation of a quark-antiquark pair inside a hadron, are not accounted for. Therefore one can only measure, not calculate, probabilities of finding a quark or gluon inside a hadron, in most cases in dependence on the kinematical situation. These probabilities are called parton density functions and will be discussed later. Similarly, the probabilty of a quark or gluon giving rise to a specific hadron can only be measured; the corresponding functions are called fragmentation functions. Both the pdf and the ff have, however, scaling properties that can be calculated.
   
   
   
2. Asymptotic freedom: The "what" and the "why"
   
3. How to measure &alpha_s