QED

QED Lagrangian

1. Full form of the QED Lagrangian
   
2. Mass of the Photon field
   
3. Intermezzo 1: P and C of the photon field
   
4. Intermezzo 2: Polarisation vectors of the photon field
   Solutions of the wave equation for the electromagnetic four-potential in the Lorentz gauge are given by where the four-vector ε^μ is the polarisation vector of the photon and only depends on the three-momentum of the photon since q²=0.
   
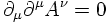
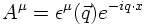
   The polarisation vector describes a spin-1 boson but has four components!
   How is this possible?
   
   First, the Lorentz gauge results in reducing the number of independent components to three.
   
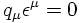
   There is still the freedom to make an additional gauge transformation: with Λ being an arbitrary scalar function satisfying so that the Lorentz condition is still valid.
   
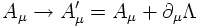
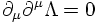
   Chosing the physics remains unchanged by the transformation This gives the freedom to set ε⁰=0 so that the Lorentz condition reads This noncovariant gauge is called the Coulomb gauge.
   
   
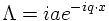
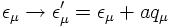
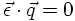
   As a consequence, there are only two independent photon polarisation vectors, both being transverse to the three-momentum vector of the photon.
   For a photon travelling in the z direction one may choose
   
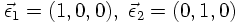
   The following linear combinations describe photons of helicity +1 or -1, respectively.
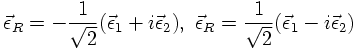
   This can be seen by considering a rotation around the z axis.
   These polarisation vectors are also called circular polarisation vectors.