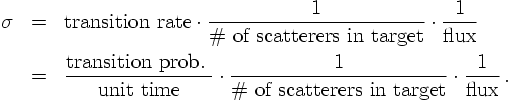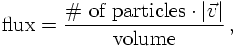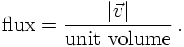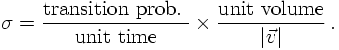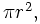Basics

S-matrix and cross sections (simplified)

  1. S-matrix and transition amplitudes
  2. Definition of cross section

    CROSS SECTION IN CLASSICAL MECHANICS

    To understand the concept of a cross section in classical mechanics first, consider the following situation: A beam of particles approaches the target under a certain impact parameter b. According to this impact parameter, dN of the particles are scattered into an angle interval [θ, θ+dθ] per unit time. To normalise, the number n of particles passing a unit area orthogonal to the direction of the beam per unit time is introduced. Then,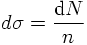
    is the corresponding classical cross section. Obviously it has dimensions of an area. It is completely determined by the scattering center and the incoming particles.
    Assuming now that the realtion of b and θ is unambigously defined - as should be the case in (deterministic) classical mechanics, particles scattered into the angular interval [θ, θ+dθ] must have approched in the impact parameter interval [b(θ), b(θ+dθ)]. The number of such particles equals the product of n with the area of this ring, i.e.
    Thus,
    Often, instead of thinking on polar angles w.r.t. the incoming beam axis, a solid angle Ω is used. To take into account such a situation, the connection of polar angle and solid angle has to be employed.

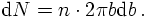
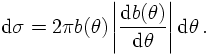
    EXAMPLE: SCATTERING OF ANOTHER PARTICLE AT REST

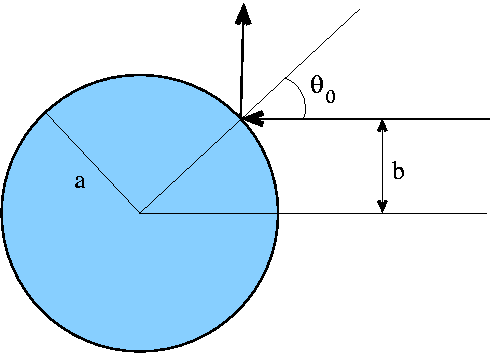
    As a fist example, consider the scattering of a beam of incoming particles off an extended, massive particle with a fixed position. The expressions above remain valid, they yield the cross section in dependence of the scattering angle in the centre-of mass system. To find the expression in terms of the scattering angle in the laboratory system, some more work is needed.
    To formulate the problem in a more formal way, consdier the scattering of particles off an absolutely hard sphere with radius a, which takes n orecoil whatsoever. The interaction law is basically given by the potential U
    Due to the geometry of the problem the trajectory of any particle can be composed from one (no scattering) or two straight lines. In the latter case, the two lines are symmetric around the radius of the sphere.
    From the sketch above,
    Therefore, in the centre-of mass sysmte, the cross section reads
    Integration over ω yields the total cross section, &pi a2, as expected.

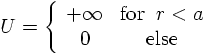
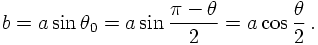
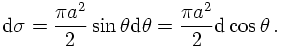
    CROSS SECTION IN QUANTUM MECHANICS

    Consider now the scattering of incoming particles on some fixed target, the classical configuration. The cross section, usually denoted by σ, is defined as the transition rate per scatter seed in the target, per normalised incident flux of scatterers. The transition rate is the transition probability per unit time, hence
    The incident flux is defined as the number of particles, n, crossing the area A during a certain time interval T. In typical scattering experiments the incoming particles are usually very carefully prepared, such that they all have nearly identical velocity v. Considering the scatter seeds (target particles) to be at rest, the normalised incoming flux is given by
    where volume here denotes the (three-dimensional) volume of space containing the particles. If there is just one incoming and one target particle, the flux thus reads
    In this simple case, the cross section is given by
    The concept of a cross section has been encountered in the framework of classical mechanics before. In the classical case, a simple example is given by a "beam" of little spheres scattering off a larger one (see above). In this case, the cross section is given by the size of the large sphere, projected onto the plane normal to the incident beam. If this large sphere has radius r the cross section therefore reads
    i.e. it has the dimensions of an area.

  3. Connection to S-matrix
  4. Cross section, luminosity, and event rate
  5. Width and life-time
  6. Problems