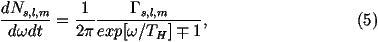
| V(r)~ |
|
|
, (1) |
| V(r)~ |
|
|
. (2) |
| rh = |
|
æ ç ç è |
|
ö ÷ ÷ ø |
|
æ ç ç è |
|
ö ÷ ÷ ø |
|
, (4) |
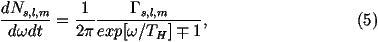
| TH= |
|
. (6) |
|
=2 |
|
|
. (7) |
|
=2 |
|
|
+ |
|
|
. (8) |
It has been suggested that since black hole formation is a non-perturbative process, the momentum scale for evaluating the pdfs should be the inverse Schwarzschild radius rather than the black hole mass. The switch GTSCA should be set to .TRUE. for the first of these options and .FALSE. for the second. It should be noted that, as confirmed in [26], the cross sections quoted in reference [10] were actually calculated with the latter pdf scale. The pdfs to be used are set using the Les Houches parameters PDFGUP and PDFSUF.
MSSDEF Conversion 1 MPLNCK=(2n-2pn-1)1/n+2Mp 2 MPLNCK=Mp 3 MPLNCK=(2n-3pn-1)1/n+2Mp
Table 1: Definitions of the Planck mass.
Name Description Values Default IDBMUP(2) PDG codes of beam particles ±2212 2212 EBMUP(2) Energies of beam particles (GeV) 7000.0 PDFGUP(2) PDFLIB codes for pdf author group -1 PDFSUP(2) PDFLIB codes for pdf set -1 MINMSS Minimum mass of black holes (GeV) <MAXMSS 5000.0 MAXMSS Maximum mass of black holes (GeV) £c.m. energy c.m. energy MPLNCK Planck mass (GeV) £MINMSS 1000.0 MSSDEF Convention for MPLNCK (see Table 1) 1-3 2 TOTDIM Total number of dimensions (4+n) 6-11 6 GTSCA Use rh-1as the pdf momentum scale LOGICAL .FALSE. rather than the black hole mass TIMVAR Allow TH to change with time LOGICAL .TRUE. MSSDEC Choice of decay products 1-3 3 GRYBDY Include grey-body effects LOGICAL .TRUE. KINCUT Use a kinematic cut-off on the decay LOGICAL .FALSE. NBODY Number of particles in remnant decay 2-5 2
Table 2: List of parameters with brief descriptions, allowed values and default settings.
Name Description Les Houches routines UPINIT Initialization routine UPEVNT Event routine Particle decays CHDFIV Generates a five-body decay CHDFOR Generates a four-body decay CHDTHR Generates a three-body decay CHDTWO Generates a two-body decay Hard subprocess and related routines CHEVNT Main routine for black hole hard subprocess CHFCHG Returns charge of a SM particle CHFMAS Returns mass of a SM particle (HW/PY) CHHBH1 Chooses next particle type if MSSDEC=1 CHHBH2 Chooses next particle type if MSSDEC=2 CHHBH3 Chooses next particle type if MSSDEC=3 CHPDF Calculates the pdfs (HW/PY) Random number generators CHRAZM Randomly rotates a 2-vector CHRGEN Random number generator (HW/PY) CHRLOG Random logical CHRUNI Random number: uniform Miscellaneous utilities CHUBHS Chooses particle energy from spectrum CHULB4 Boost: rest frame to lab, no masses assumed CHULOB Lorentz transformation: rest frame®lab CHUMAS Puts mass in 5th component of vector CHUPCM Centre-of-mass momentum CHUROB Rotation by inverse of matrix R CHUROT Rotation by matrix R CHUSQR Square root with sign retention CHUTAB Interpolates in a table Vector manipulation CHVDIF Vector difference CHVEQU Vector equality CHVSUM Vector sum
Table 3: List of subroutines with brief descriptions.
Figure 1: Parton-level energy spectra of Higgs bosons, mH = 115 GeV. Solid: predicted energy spectrum of Higgs bosons from decay of black holes with initial masses 5.0-5.5 TeV. Dashed: neglecting time variation of temperature. Dot-dashed: neglecting grey-body factors.
Figure 2: Parton-level energy spectra of electrons and positrons. As Figure 1 but for electron and positron spectra.
Results of a fuller study of signatures of black hole production and decay at the LHC will be presented elsewhere [32].
Figure 3: Parton-level energy spectra of photons. As Figure 1 but for photon spectra.
This document was translated from LATEX by HEVEA.