QCD

Multiple gluon/parton radiation


  1. e+e-→ hadrons at higher orders
  2. Jets
  3. Large logarithms and splitting functions
  4. Resummation/exponentiation
    There are two ways to sum the leading logarithms, an elegant one and a brute-force one. Here the second appraoch will be chosen, resulting in explicitly summing the leading logarithms. As an example case, of course again our prime example, ee→ qqg is chosen again.

    LIGHT-CONE VARIABLES

    Let us start by introducing light-cone variables. They are defined in the following way:
    1. Take any two vectors, in our case p2 and p3 and define a common (z-) axis, its spatial component points in the direction of the sum of the two vectors.
    2. Define transverse components of each of these vectors to be taken w.r.t. this axis, see the figure below.
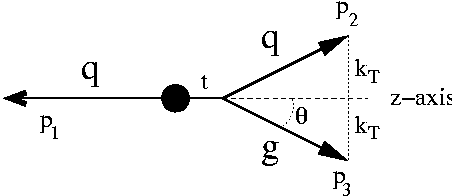
    3. There are two other directions, called the "+"-and the "-"-direction. The two vectors are completely determined by these two components given by (E± pz).
    In other words consider the transformation from the original vectors
    to
    Due to momentum conservation, in the c.m. frame of the photon the sum of the z-components of the antiquark- and gluon-momentum equal the negative z-component of the quark momentum conservation. Therefore,
    This motivates to normalise both the "+"- and the "-"-components on the total energy and to call them x±:
    Then, similar reasoning as above and the use of the previously defined energy fractions x yields
    Here t is the invariant mass squared of the antiquark-gluon system. Also,
    which is identical for both particles. Also,
    and
    The last relation is a bit tedious to prove, it is left to the reader as an exercise.

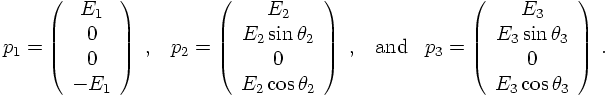
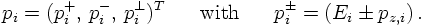
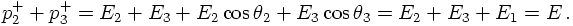
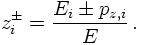
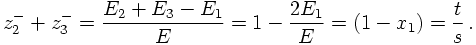
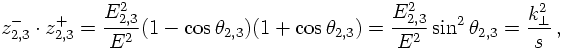
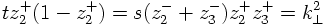
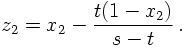
    USING LIGHT-CONE VARIABLES: LEADING LOG APPROXIMATION

    The light-cone variables introduced above are now used to rewrite the matrix element for ee→qqg in terms of z=z2+ and t: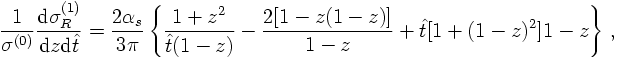
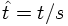
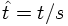
    where the dimensionless quantity
    has been introduced. Simple consideration now show that it is in fact the first term in the expression above for the differential cross section, which dominates the total cross section, since it has two poles rather than one. Taking a closer look at it, it can be seen that it is in fact dominant in the region of small transverse momenta, i.e. when
    becomes small. Retaining only this first term is also known as the leading pole approximation, when integrated over t, however, it produces the leading logarithmic singularity. This singularity in fact is twofold, therefore one often calls this approximation the double leading log approximation (DLA). Anyways, integrating in suitable bounds, this double leading log is readily found:
    where in going from the first to the second line it was implicitly assumed that the boundaries of the z-integration are only little different from [0,1]. Two things should be noted already here:
    1. In most cases, the bounds of the z-integration depend on the actual value of t'. There is a simple reason for this. In principle, the treatment here does not take into account recoil effects. However, as soon as the notion of a resolution parameter is introduced, the invariant mass t' of the decaying parton/produced qaurk-gluon system together with this resolution parameter implies some conditions on the z parameter. This will be elucidated later.
    2. Also, as we have seen before, the coupling constant is running and one has to make a choice for the relevant scale. This choice will, of course, depend on the kinematics of the splitting, i.e. on t' and z'. In fact, it has turned out that the transverse momentum in fact is the best choice for this. In any case, α would be inside the integration.


    SUMMING LEADING LOGS

    Rather than trying to sum the emerging logs now by employing theoretical arguments, let us analyse and interpret the structure of the expression above. Simple considerations tell us that the 1/t' term looks like the propagator of a massless particle - in fact, it is the propagator of the "decaying" particle. Similarly, the splitting function is a local approximation of the full amplitude, projected on the piece where a specified quark line decays into quark and gluon. In other words, it is something like a "decay amplitude" squared.
    Let us formulate this in yet another fashion: in fact there are two quark lines (quark and antiquark) that could emit a gluon. In the language of Feynman diagrams, these two diagrams/amplitudes would have to be summed before squaring them. By going to the soft and collinear limit (collinear w.r.t. one quark line), as done above, the effect of the other quark line vanishes and typical quantum interferences are suppressed. It should be stressed here that this interpretation is a very pictorial one, written in the language of Feynman diagrams one still has a freedom of gauging the gluon field, where specific gauges support or destroy this simple interpretation. Anyways, choosing a type of gauge called the axial gauge, one can choose a gauge vector (axis) such that there is a clear and unambigous way to tell which one of the two diagrams gave rise to the leading pole.
    However, having at hand this interpretation of a decaying particle, it is simple to try to iterate this process of gluon emission by one of the quark lines. Including in a proper way the running of α one thus finds
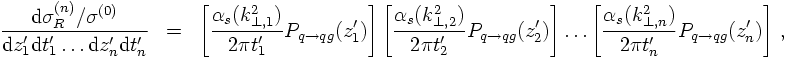
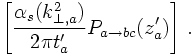
    where the splitting functions have duly been included. It is easy to generalise this expression such that it includes all possibilities. Just notice that the probability for any parton a to propagate with invariant mass squared t' and to decay into apair of partons {bc} is given by

    In order to have maximally large logarithms it is easy to understand the various t' are ordered such that
    Here the resolution cut-off for the t' has been introduced and obviously s, the c.m. energy squared is the largest possible scale in the process. Note here that by choosing "large" values for the t the realm of soft and collinear emission is partly left. This ordering leads to nested integrals. However, before addressing this point and finding a simple solution, let us make a little detour.

    ANGULAR ORDERING

    Let us turn for a second to the case of QED radiation and consider a virtual photon splitting into an electron-positron, which in turn emits another photon, see below.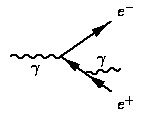
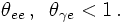
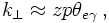
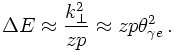
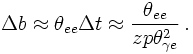
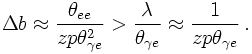
    Assume now that all relevant angles are small - the collinear limit - i.e.
    Then the transverse momentum of the radiated photon w.r.t. the emitting positron is given by
    where p is the relevant positron momentum and z is the splitting variable. Therefore, the "energy imbalance" at the photon-positron vertex is
    Due to the uncetainty principle, this is the inverse of the time available for the photon emission. In this time the electron-positron pair will separate by
    In order for this splitting process to happen, the photon must be able to resolve the transverse separation and, thus, the two independent charges (if the photon does not resolve them, the net charge is zero, and hence there is no photon radiation). This resolution will happen only, if the transverse separation of the pair is larger than the transverse wavelength of the photon,
    This immediately implies an angular ordering of the subsequent emission, i.e.
    in order for the secondary photon radiation to happen. This effect is known as the Chudakov effect, and it is a direct consequence of the quantum nature of the emission process.
    In QCD, life is a bit more complicated. This is easy to understand by just replacing the photons with gluons and the electron-positron pair by a quark-antiquark pair. The main difference here is that the net colour charge of the quark-antiquark pair differs from zero, hence they can emit the extra gluon coherently. This however can be interpreted such that the initial gluon emitted the extra gluon before splitting into a quark-antiquark pair. Taken together, in this case there are two options
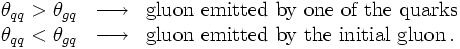
    In other words: Quantum coherence implies angular ordering.
    Quantum coherence is modelled best by using the opening angle or the transverse momenta of the pairs produced in parton splitting rather than using the invariant mass squared of the decaying partons. The choice of transverse momentum as the relevant scale for the splitting in the coupling constant motivates to use also transverse momenta instead of the t'. Simple calculation indeed shows that in the soft-collinear limit, the propagator term is roughly given by the transverse momentum squared. in fact, a more careful analysis of the QCD radiation pattern including the effect of quantum coherence shows that employing such an ordering in transverse momenta (rather than in masses, as above) allows to take into account not only the doubly leading logarithms but also the most relevant single logs. This is known as the modifield leading log approximation (MLLA).

    RESUMMATION AND THE SUDAKOV FORM FACTOR

    Let us now return to the expression above for multiple gluon emission. When replacing the virtual masses with the corresponding transverse momenta, the limits of the z-integration can easily be fixed. This allows to define the integrated splitting function, aka the branching function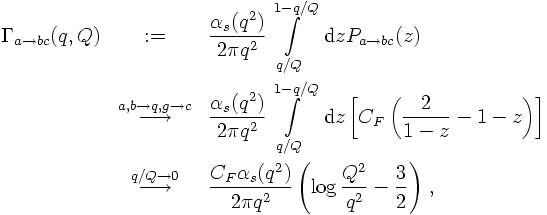
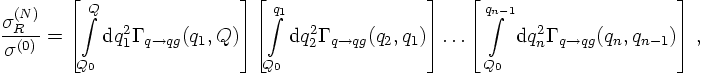
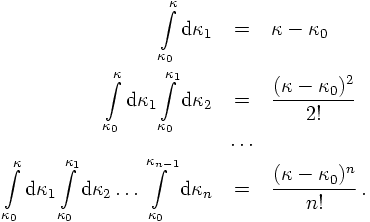
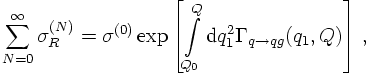
    where the q stand for transverse momenta and where in going from the first to the second line the splitting function has been specified as the one responsible for q→ qg. Therefore, one can write
    where the ordering in transverse momenta has been made explicit. This looks horrendous, but in order to see what's going on, let us check some simpler integrals, basically without any function to integrate over. There
    Summing over all n leads to an exponential. By analogy this implies that
    where only one quark line has been included. This expression obviously resums all possible number of resolvable gluon emissions from the quark line at the leading logarithmic level.
    It is then simple to see that the inverse, known as the Sudakov form factor
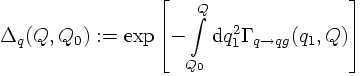
    describes the probability for no resolvable emission from the quark line between the two scales. This looks like a horrendous expression, but in fact it is rather useful, as will be seen in the next section.

    NLL JETRATES IN ee→ hadrons

    Coming back to the interpretation of the Sudakov form factor it is now easy to construct expression for resummed jet rates at MLLA accuracy. For instance, the two-jet rate in ee-annihilations at the level of quarks and gluons is just given by the probability that neither the quark nor the antiquark emit a resolvable gluon. Choosing now a jet definition based on transverse momenta, like, e.g. the Durham scheme, it is clear how this connects with the Sudakov form factors: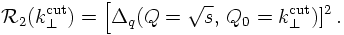
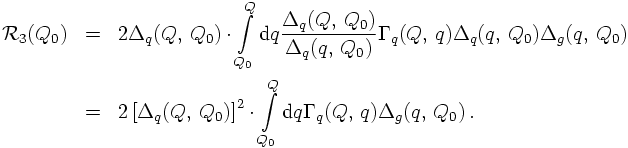
    The two-jet rate, as said before, is just the product of the no-splitting probabilities of the quark-lines between the relevant scales. The three-jet rate is a bit more complicated to get at. In this case, there are two possibilities of the same kind. One quark line does not split, whereas the other one splits exactly once, somewhere between the c.m. energy and the jet-resolution. Thus,
    The surprising thing in the first line may be the occurence of the ratio of Sudakov form factors. However, a little thought shows that this ratio is nothing but the probability for having no emission between Q and q, resovable at the jet resolution scale. In a similar, straightforward fashion, higher order jet rates may be recovered, leading to increasingly long expressions. They can be constructed either "by hand" as exercised here or through generating functionals. However, the next plots show that these comparably simple way of estimating jet rates is in amazing agreement with data.

    SIMULATIONS

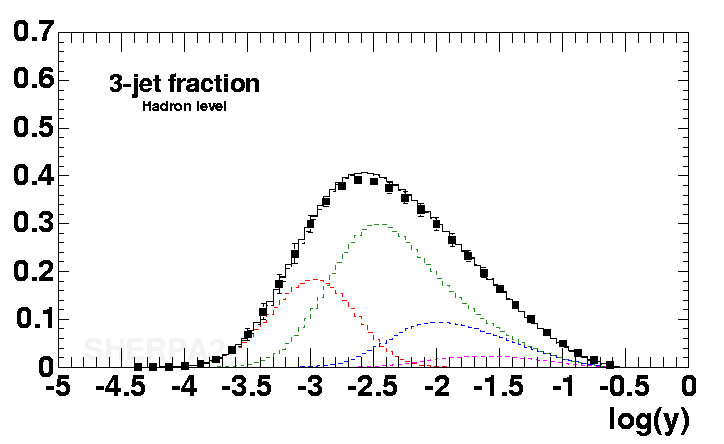
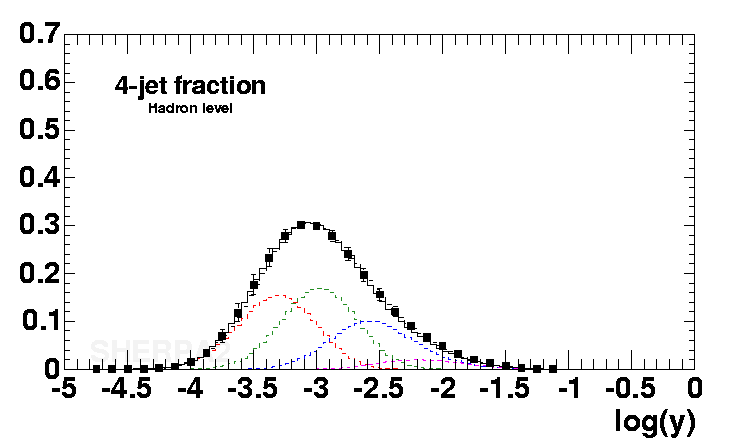
    The probabilistic interpretation of the Sudakov form factor lends itself a way to a simulation of the multiple emission pattern of QCD radiation. Such simulations have a Markovian structure - they can be set up in a recursive fashion with (up to kinematics) independent emissions. In such simulations, aka parton showers, starting from a scale Q, the next emission at scale q is recovered by equating a ratio of Sudakov form factors (exactly like the one above) with a random number. Since this ratio gives the probability for no resolvable emission between the two scales, one minus this ratio yields the probability for having an emission at q. Thus equating this ratio with a random number and solving for q yields the correct distribution of QCD radiation in terms of transverse momenta.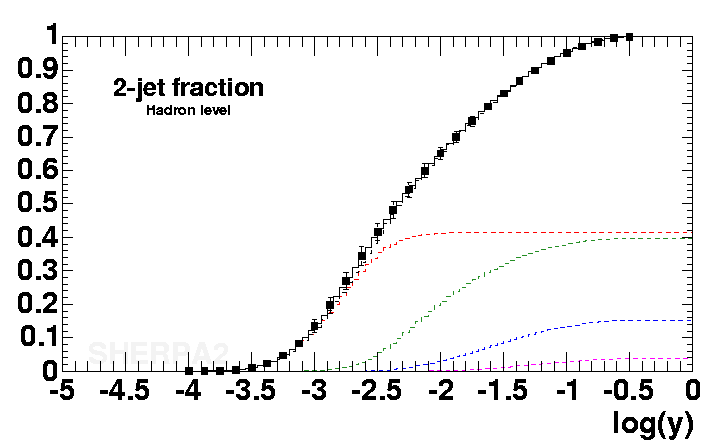
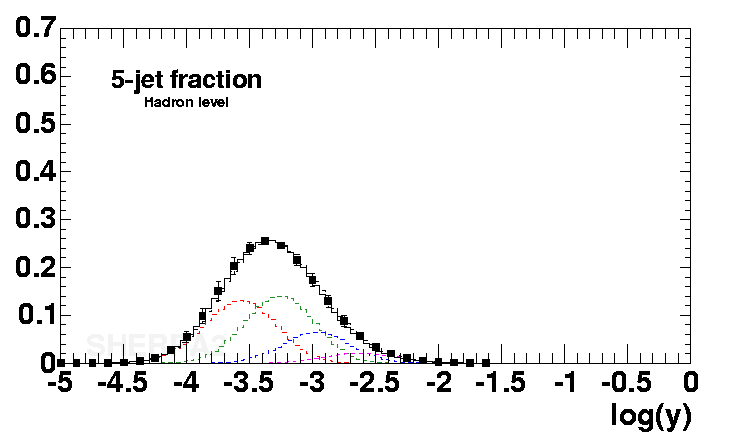    In the plots above, y is the square of the resolution cut divided by the c.m. energy. The c.m. energy is 91.2 GeV (LEP1), thus y=0.01 corresponds to transverse momenta of 9.12 GeV, y=0.0001 corresponds to transverse momenta of 0.9 GeV. In all plots above, data (the boxes) are from LEP1, and can be found in a publication by Pfeifenschneider et al.. The black line is a simulation by Sherpa.


  5. DIS: Deep inelastic scattering and the DGLAP evolution equation
  6. Drell-Yan processes at hadron colliders