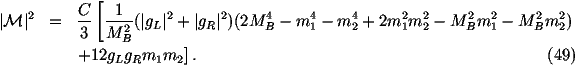Tutorial on Writing Simple Event Generators and the Les Houches Accord
P. Richardson,
Theory Division, CERN, 1211 Geneva 23, Switzerland.
Table of Contents
1 Introduction
The aim of this tutorial is to enable people to write their own simple
parton-level generators and interface them to either HERWIG [1, 2]
or PYTHIA [3, 4]
via the
Les Houches Accord. It contains both the information you need to construct a simple
parton-level
Monte Carlo event generator and the necessary information needed to use the Les Houches Accord. After reviewing the Monte Carlo technique we will discuss how combine
the calculation of the phase space and matrix element to produce
a program to generate parton-level events. We will then discuss how to combine this
with the general purpose event generators.
2 Monte Carlo Technique
The Monte Carlo procedure is based on the following result.
For a simple one-dimensional integral,
The average, á f(x) ñ, can be approximated by
calculating f(x) at N
randomly chosen points, in the interval (x1,x2), i.e.
giving an estimate,
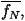 of the average. This method
is particularly
useful as we can also calculate an error on the estimate by computing
the standard
deviation and applying the central limit theorem
where
of the average. This method
is particularly
useful as we can also calculate an error on the estimate by computing
the standard
deviation and applying the central limit theorem
where
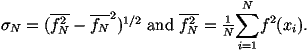
The convergence of this method for numerically evaluating the integral
goes as
1/N1/2 with the number of function evaluations, N.
This is slower than other commonly used
techniques for numerical integration, e.g. the trapezium rule converges as
1/N2 and Simpson's rule as 1/N4.
While the convergence of these other methods becomes far slower for higher
dimensional integrals, e.g. the trapezium rule converges as
1/N2/d and Simpson's rule as 1/N4/d where d is the dimension of
the integral, the Monte Carlo method will always
converge as 1/N1/2.
Hence for the performance of high-dimensional integrals the Monte Carlo
technique is
more efficient. This is particularly important in particle physics where
we need to
perform high dimensional phase-space integrals. The Monte Carlo procedure
is also well
suited to integrating over complex regions, which are difficult with
other methods, and
often occur in particle physics, e.g. due to experimental cuts.
Another advantage of
this method is that we can evaluate a number of different quantities, e.g. differential distributions, at the same time whereas with other methods
each distribution
would have to be calculated separately.
In practice we always generate the integration variable
uniformly between its limits. This allows us to construct a weight
which will average to give the integral we are calculating.
Often we will make a change of integration variables so that the
variance is reduced and the integral converges faster towards the true
answer.
In general we will split the weight into a number of pieces which are multiplied
together at the end in which case we will often combine the part of
the weight coming from the integration limits
and the phase-space factors and compute this separately
to the matrix element piece which contains information specific to the
process we are generating.
Another useful property of the Monte Carlo procedure is that we can generate
unweighted events, i.e. processes that occur with the same probability as
in nature. To do this all we need to do is compare the weight
we calculate for a specific phase-space point with a random number
uniformly distributed between zero and the maximum possible weight.
If the weight is bigger than the random number we keep that
phase-space configuration as an unweighted event. This is
particularly useful in particle physics as we can then
pass the unweighted events through a simulation of the detector
and compare predictions with data.
In the next section we will discuss how to write a simple parton-level
generator followed by a discussion of how to run this with either
HERWIG or PYTHIA.
3 Parton Level
The first thing we need in order to construct any Monte Carlo program is a
random number generator. You may have your own program for this or you can get
the random number generator
from HERWIG, (see Appendix B.1.)
The next thing is to decide how to
construct the program. The best way to start is with a simple main program and
a routine to calculate the weight for the integral of the matrix element. This
routine will first generate a phase-space point and then calculate the matrix element
at that phase-space point.
This program should specify the basic input parameters. In
our case there are a number of parameters:
-
The type of incoming particles. As we are working with hadron-hadron collisions
this will probably be either protons or antiprotons;
- The energy of the incoming particles;
- In hadron-hadron collisions we also need to specify
the parton distribution functions we wish to use.
There are a number of ways we could specify these parameters, however as we will
be using the Les Houches Accord to pass events to an event generator
eventually the best option is to specify these via the Les Houches run common block,
you can get the code for this common block in Appendix B.2.
At this point we only need to specify:
-
The beam energies in GeV via the variables
EBMUP(1,2) for the two beams. The first beam is assumed to be travelling
in the positive direction along the z-axis while the second beam is
assumed to be travelling along the z-axis in the opposite direction;
- The types of the beam particle, IDBMUP(1,2), using their PDG [5] codes.
In practice we are only dealing with protons (code=2212)
and antiprotons (code=-2212);
- Which parton distribution functions (PDFs) you wish to use.
In the Les Houches Accord this is supposed to be specified using the
author code and PDF set code from PDFLIB [6]. I have supplied a simple
routine (see Appendix B.3 which will allow the use of
either the default PDFs
built into either HERWIG or PYTHIA or one of the sets in PDFLIB. In practice I would
recommend that you use either the default sets PDFGUP(1,2)=-1,
PDFSUP(1,2)=-1 or the leading-order set of
CTEQ51
PDFGUP(1,2)=4 and PDFGUP(1,2)=46.
It is often useful to set certain cuts at this point, for example a cut
on the partonic centre-of-mass energy for resonance production or the rapidity
for heavy quark production at this point. You may also wish to decide
which processes to generate, so that for example only the leptonic
decays of the resonance are included. An example program with this done
is described in Appendix B.4.
The next step is to calculate the masses, couplings and widths of any new particles
predicted by the model we are simulating. We will be using the Little Higgs Model
as an example and therefore you need a routine to calculate the particle
properties in this model. The model and how to do this are discussed in
Appendix A.
The next thing is to decide how to generate the phase space for the process you are
interested in. We will consider 2®2 scattering processes. In practice for these
processes in hadron-hadron collisions there are two phase-space mappings
which are likely to be useful. The first is designed to smooth out any
resonances and rises at small values of the parton-parton centre-of-mass
energy due to photon exchange while the second is useful for QCD type processes.
In the Little Higgs model there are examples of both type of process, i.e. the resonant
production of new heavy gauge bosons followed by their decay to
Standard Model fermion-antifermion pairs and the production either singly or
in pairs of the new heavy top quark predicted by the model.
In the following section there are instructions on how to write an event
generator for these processes.
I'm sorry but I've only written the
resonances so far. I'll try and add the heavy top production soon.
3.1 Resonance Production
In this section we will discuss how to write an event generator for resonance
production. We start by discussing how to generate the phase space and then
how to calculate the matrix element.
3.1.1 Phase Space
The cross section for a 2®2 scattering process in
hadron-hadron collisions can be written as
for the process 12®34 where
s^ is the parton centre-of-mass energy squared,
p1,2 are the 4-momenta of the incoming particles,
p3,4 are the 4-momenta of the outgoing particles,
Ei is the energy of the ith particle, x1,2 are the fractions
of the momenta of the incoming beam particles carried by the
incoming partons, fi(xi) are the parton distribution functions
and åspins
|M|12®342 is the matrix element squared for the
process averaged over the spins and colours of the incoming particles
and summed over the spins and colours of the outgoing particles.
First we perform the integral over the 3-momentum of p4 and reexpress the integral
over the momentum of p3 in terms of the magnitude of the three-momentum
p in the centre-of mass frame, the angle with respect to the beam q
and azimuthal angle f. This gives
We can write the argument of the d-function as
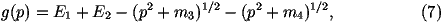
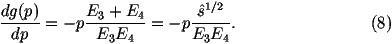
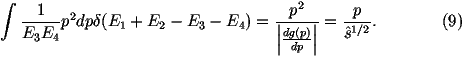
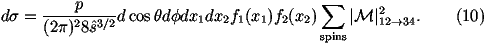
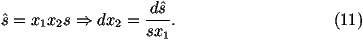
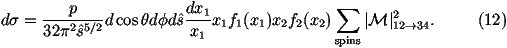
Let's consider this piece by piece:
-
The angular integrals are trivial we will pick a value of f
randomly between 0 and 2p and cosq randomly between
-1 and 1. Therefore the weight of the angular part of the integral is 4p.
- The tricky part is how to distribute the values of s^.
Here we are assuming that there will be peaks in s^ either when
massive intermediate particles are on mass-shell or s^ goes to zero
due to photon diagrams.
First we need to impose some minimum value of s^ to regulate the integral
so we are performing the integral
where smin^ is the minimum value of s^ and
s is the centre-of-mass energy squared of the hadron-hadron collision.
In order to smooth the peaks in the integrand it is useful to define a function
where wi is a weight between zero and one such that åi wi=1 and
In practice we will use two types of function:
-
The first is designed to smooth out
a Breit-Wigner resonance
where Gi is width of the resonance and Mi is its mass;
- While the second is designed to smooth out the rise in the cross section due to
photon exchange at small centre-of-mass energies
where ai is the power for the smoothing, in practice ai=2 is usually
a good choice. The value of ai should always be chosen to be
less than 1 in the mapping we are using.
Having defined this function we can rewrite the integral over s^ as
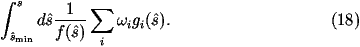
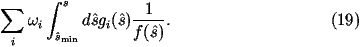
-
First we use the weights wi to select one of the terms in the series. To do this we:
-
Generate a random number between 0 and 1;
- Compare this random number with the first weight;
- If the random number is less than this weight then we select this channel,
otherwise we subtract the weight for this channel from the random number
and go on to the next channel;
- Repeat the previous step until we have selected one of the channels.
This procedure is designed to pick a given channel, i,
with probability given by wi.
- Perform a transformation to smooth the behaviour of that term.
-
If we are smoothing a Breit-Wigner distribution we define
This gives
We can then generate ri uniformly between
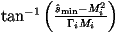 and
and
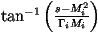 .
The value of
s^ can be calculated from ri using
The weight for the integral is then obtained by replacing dri with the difference
in the limits which will cancel with the denominator giving 1.
.
The value of
s^ can be calculated from ri using
The weight for the integral is then obtained by replacing dri with the difference
in the limits which will cancel with the denominator giving 1.
- If we are smoothing a power law we define
This gives
We then generate ri uniformly between s1-ai and
s^min1-ai. The value of
s^ can then be calculated from ri using
The weight for the integral is then obtained by replacing dri with the difference
in the limits which will cancel with the denominator giving 1.
- Having generated s^ as described above we can compute the value of f(s^).
This allows us to compute the weight for the s^ integral, i.e.
Let us now consider the Little Higgs model. In this model we may wish to simulate
the resonant production of either the additional heavy W bosons or the additional
heavy Z and photon. Let us consider these two cases separately:
-
For the simulation of the heavy W we will want two channels to smooth the
Breit-Wigner peaks from the Standard Model W and the new heavy W predicted
by the Little Higgs model;
- For the simulation of the heavy Z and photon we will need three channels
to smooth the Breit-Wigner peaks for the Standard Model Z and the new
heavy particles. We will also need one channel to smooth the rise
in the cross section at small masses due to photon exchange.
At the moment I have only written the code for the second case and therefore
you should do that one.
- This only leaves the value of the momentum fraction x1 to be generated. The easiest way to generate the momentum fraction is to perform a transformation on the integral giving
where r=lnx1. Therefore we randomly generate r between ln(s^/s) and 0. We can then obtain the value of x1 using x1=expr. The weight of the integral is -ln(s^/s).
If we put all this together then the weight for the integrals is


-
The parton distributions are usually returned multiplied by the
momentum fraction and therefore it is useful to include this factor
with the PDFs.
- As we have generated cosq, f, s^ and x1 nothing
depends on the masses of the final-state particles apart
from the outgoing momentum in the centre-of-mass frame and
the matrix element. This means that if we include the
momentum with the matrix element we only have to
generate one phase-space point for all the different decay modes
of the bosons.
This only leaves the matrix element part of the total weight to calculate
We will discuss the calculation of this in the next section.
3.1.2 Matrix Element
We can write the general matrix element for the process ff_® f'f'_ via
the exchange of an s-channel spin-1 gauge boson as follows
where t^=(p1-p3)2, u^=(p1-p4)2, m3,4 are the masses of
the outgoing particles and the couplings are defined to be2
where the sum runs over all the gauge bosons which can contribute to the process,
Mi is the mass of the boson, Gi is the width of the boson,
g1L,R is the coupling of the gauge boson to the incoming fermions and
g2L,R is the coupling of the gauge boson to the outgoing fermions.
These couplings are given in Table 1 for the Little Higgs
model.
We are now able to calculate the matrix element part of the weight.
For the production of the neutral gauge bosons we can economize on the number
of channels we need to calculate in the following way. First the matrix
elements for all incoming down type quarks will be the same, as will the matrix
elements for all incoming up type quarks. We then need the matrix element for
all the different Standard Model fermions as outgoing particles.
So we will start by looping over the two different types of incoming particle,
i.e. dd_ and uu_. We will then loop over the final-state particles.
For each combination we will first check whether s^>(m3+m4)2. If this is
true we need to calculate the matrix element, if s^<(m3+m4)2 the mode is
kinematically forbidden. We start by using
the couplings given in Table 1 and the masses and widths
of the gauge bosons to compute the couplings gab as
complex numbers.
We can then compute the magnitude of the momentum of the outgoing
particles in the centre-of-mass frame using
to compute the centre-of-mass momentum of the outgoing particles.
The values of t^ and u^ can then be computed using
where Ei=(pcm2+mi2)1/2.
You can now combine the couplings and the kinematic variables to
compute the matrix element.
All that remains is to is combine the matrix element with the parton
distribution functions. Again we can use a trick improve efficiency.
We have computed the matrix element for qq_® ff_ and the weight
for this is
Where we have still to include the PDF factors.
This is the weight of a quark from the first beam and an antiquark from
the second beam. We also need the weight for an antiquark from the first
beam and a quark from the second beam. In principle we should recompute
the matrix element with the opposite value of cosq because
changing the order of beams is equivalent to changing the sign of
cosq. In practice we will use the same matrix element
but use the opposite sign of cosq when we reconstruct the momenta.
We must remember that we have only calculated the matrix element for either
dd_ or uu_ initiated production. Therefore as well as multiplying by the
PDFs for the type of quark we have used we must also use the other quarks of
the same type, i.e. ss_ and bb_ as well as dd_ if
we started with the matrix element for dd_ initiated production.
Therefore when we combine with the PDFs to produce the total matrix element part of the weight
we should have
for a quark from the first beam and
for an antiquark from the first beam. You should remember when constructing this weight that
the PDF routines will return xf(x) and not include it twice.
In total we should have the matrix element weight for:
-
6 incoming quark types:3
- 2 orders of the incoming particles, i.e. quark or antiquark from the first beam;
- 12 outgoing fermions.
In practice you may only be interested in some of the possible outgoing fermions,
for example the charged leptons, in which case there is no need to calculate the
weights for all the possible outgoing fermions.
It is good practice to both add all of these up to calculate the total matrix
element weight and store the values for each case in an array.
Having done this the only remaining thing to do is calculate the total weight
by multiplying by the phase-space part of the weight.
We must remember that this weight is in GeV-2 and
convert it to some more suitable units. The Les Houches Accord states we should supply
cross sections in picobarn so we must multiply by the conversion
constant 3.89379×108 GeV2pb.
You can now compute the total cross section and its error by generating a number
of weights. The average will be an estimate of
the cross section and s/N1/2 an estimate of the statistic error, where
s is the standard deviation. This is described in the introduction.
A version of the example program including this is described
in Appendix B.7.
At this point we can also produce histograms of interesting quantities. An interesting example is to fill a histogram with s^1/2 on the x-axis and the weights on the y-axis and only generate e+e- as the outgoing particles. If you divide the contents of each bin by the total number of weights and the size of the bins then you have a plot of the differential cross section with respect to s^1/2. An example of this is shown in Fig.1 from the example program together with the Standard Model result from HERWIG with the same Standard Model parameters.
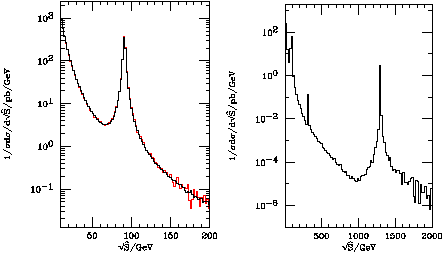
Figure 1: 1/sds/ds^1/2 for the production of e+e-
with f=2 TeV and q=q'=p/4 at the LHC.
The black line is the
result of the example program and the red line the result from HERWIG
for the Standard Model with the same Standard Model parameters.
The first plot shows the agreement in the low mass region whereas
the second plot shows the new AH and ZH resonances
at 316 GeV and 1.3 TeV respectively.
3.1.3 Generation of the Momenta
As a final step if we want to use the code as an event generator we must
assign both a momentum configuration and the particle types.
The momenta of the incoming particles are given by
where we have assumed the hadron-hadron collision is occurring in the
hadron-hadron centre-of-mass frame and the four-vectors have the form
(px,py,pz,E), which is commonly used in event generators. The event generators
often have a fifth component in the vector which gives the mass of the particle
and it is useful for us to do this as well.
We also need to select the types of the incoming and outgoing particles.
We can do this in a similar way to the one we used at the beginning to
select which of the integration channels to use. We start by generating a
random number between 0 and 1. We need to define a new variable, PW,
which is the matrix element part of the weight multiplied by this
the random number.
We can then loop over all the weights for the particular incoming and outgoing
particles, and order of the incoming quark and antiquark. For each case we compare
PW with the weight of the given channel. If PW is
less than the weight for the channel we select that channel otherwise we subtract
the weight of the channel from PW and keep going. Eventually we will
have selected a particular channel.
We then have the identities of the incoming particles and outgoing particles.
We must change the sign of cosq if the first incoming particle
is an antiquark.
We then need to calculate the momenta of the outgoing particles.
We first need their momenta in the centre-of-mass frame which is given by
where m3,4 are the masses of the outgoing particles.
The momenta of the outgoing particles are then given by
These momenta need to be boosted from the parton-parton centre-of-mass frame to
the centre-of-mass frame of the hadron-hadron collision.
A simple set of routines to do this can be found in Appendix B.8.
We will discuss how to put these events in the Les Houches event common
block in the next section either for parton-level analyzes or as a prelude
to interfacing with the general purpose event generators in the next section.
3.2 t-channel Production
I will hopefully add a t-channel example soon
3.3 Entering Particles in the Les Houches Event Common Block
We now know both the momenta of all the particles and their identities.
In order to do any form of analysis we would now want to use these
momenta to look at physical quantities. This means we need to pass momenta and particle
identities to an analysis routine.
There are many ways we could do this but the best one for our purposes is to use the
Les Houches Accord event common block. The code for this can be found in
Appendix B.9.
We should first set the total number of particles NUP to the number of particles.
In the resonant production example this will be 5 as we will add the
intermediate resonance as an extra particle while for the t-channel example
it will only be 4.
First we enter the incoming bean particles we should therefore:
-
Set
the status, ISTUP of the first two entries in the Les Houches common block
to -1 for incoming particles;
- Set the identities, IDUP of first two entries to the identities of
the incoming particles;4
- Copy the 5-component momentum of the incoming particles into the first two records
in the Les Houches momentum array, PUP. The first index of the
PUP array is the component of the momentum whereas the second index is the
particle.
For the resonance production we need to add the resonance to the event record in
the following way:
-
Set the status ISTUP(3)=2, this status is important for interfacing
with the event generators and will ensure that the event generator
preserves the invariant mass of the resonance;
- Set the mothers of the particle MOTHUP(1,3)=1,
MOTHUP(2,3)=2;
- Set the 5-momentum of the particles to the sum of the momentum of the
outgoing particles. The first four components should be the sum of the
incoming particles while the 5th component should be s^1/2.
We then need to add the outgoing particles in next two free entries in
the common block in the following way:
-
Set the status of the particles, as they are outgoing, ISTUP(I)=1;
- Set the mothers of the particles, MOTHUP. For the case of resonant production
this should be the location of the resonance,i.e. MOTHUP(1,I)=3, while
for the t-channel example it should be the the locations of
the incoming particles MOTHUP(1,I)=1,
MOTHUP(2,I)=2;
- Copy the 5-component momentum of the outgoing particles into the
relevant entries of PUP.
In order to use the general purpose event generators we also need to define a colour
flow. This is discussed in more detail in [7]. As we are only dealing
we the simplest case at the moment the colour flow pointers should be set such that
ICOLUP(2,I) for the incoming antiquark and ICOLUP(1,I) for the incoming
quark
are set to the same value, it does not matter what this value is as long as it is
non-zero. Similarly if the outgoing particles are coloured their pointers should be
set in the same way to a different non-zero integer.
All the other values of ICOLUP should be zero.
We now have a simple parton-level generator that we could use to do parton-level analyzes, an example of this program is discussed in Appendix B.10.
Rather than discuss the use of this program in detail we will now go on
and interface this to one of the general-purpose event generators for
a full simulation of the event.
4 Interfacing with General Purpose Generators
We have now written a program which is capable of generating parton-level events.
This need to be interfaced with one of the general-purpose event generators.
In order to do this we need to do two things:
-
Unweight the events;
- Pass them to the generator.
There are two ways to do each of these. We can either unweight the events
ourselves and then pass them to the event generator, or we can passed the
events with a weight and leave the unweighting to the event generator.
Similarly we can either output the events as a file and then read the
file into the event generator or we can directly link the code with the
event generator. We will discuss both of these options.
4.1 Linking with the Generator
If we wish to link directly
with the generator then the easiest thing is to let the
generator handle the unweighting
of the events.
In that case we need to modify the main program into an initialization
subroutine, this routine should be called UPINIT.
This subroutine should calculate a reasonable number of events,
say 10000, to get an initial estimate of the cross section and the error.
It should also keep track of what the maximum value of the weight was.
We can then use this information to set up the event generation via the
Les Houches Accord run common block. We need to set:
-
The number of processes NPRUP, well at the moment we only have
one;
- An identity code for this process, LPRUP(1), you can pick anything
you like;
- The value of the cross section XSECUP(1), you should set this to the
value you have calculated;
- The error on the cross section XERRUP(1), you should set this to
the error you have calculated;
- The maximum weight for the process XMAXUP(1), which should be
set to the value you have calculated;
- We also need to tell the generator what we want it to do
with the events. There are a number of options, however we need to
use IDWTUP=1 or IDWTUP=2 which both take weighted
events and produce unweighted events.5
We also need a routine which will be called to generate an event, UPEVNT.
In our case all this routine need to is call your routine to calculate the
weight and set the value of XWGTUP in the Les Houches event common
block to the weight.
You are now ready to link your code with one of the general purpose event generators.
You will need either HERWIG which is available from
or PYTHIA which is available from
You should remove the dummy Les Houches Accord subroutines UPINIT and
UPEVNT as well as the dummy PDFLIB subroutines PDFSET and STRUCTM
from these programs and then compile and link them with your code.
An example program to do this is described in Appendix B.11.
4.2 Outputting the Events as a File
I'll try and write this soon
5 Conclusions
Hopefully you have found this tutorial useful. If you have any problems or question them please let me know.
A Little Higgs Model
We will use the Little Higgs Model as an example, using
the formalism given in [8]. In order to specify the properties
of this model we need to define a number of additional parameters:
-
In the Little Higgs model there are new U(1) and SU(2) gauge groups.
The mixing of the gauge couplings for these groups with the normal Standard
Model groups must be specified. In practice this amounts to specifying the mixing angles s=sinq for the SU(2) group and s'=sinq' for the U(1) group.
- The symmetry breaking scale f and the vacuum expectation value for the
breaking of the new groups, v'. These can be roughly related to the Standard Model VEV by v'/v£ v/4f.
- The couplings in the Higgs sector6 which can be traded for the Higgs mass and VEVs.
- The new top Yukawa coupling which can be replaced by the mass of the heavy top quark, MT.
In order to use this model we need to calculate the properties of the particles from these parameters and the parameters of the Standard Model.
You should start with a piece of code that specifies the parameters:
-
The properties of the Standard Model, i.e. MW, MZ, a,
sinqW and the masses of the Standard Model fermions;
- The mixing angles q and q';
- The mass of the new heavy top quark;
- The new parameters f and v', we can use the approximate relationship, v'/v£ v/4f, to calculate v'.
We can then calculate the other parameters, couplings and particle properties. We need
-
Standard Model couplings e=(4pa)1/2, g=e/sinqW,
g'=e/cosqW, v=2MW/g.
- The Yukawa couplings, l1,2, of the top quarks using
where mt is the mass of the top quark.
The value of l2 can be obtained by replacing ± with
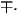
- The masses of the new heavy gauge bosons
where
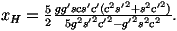
- We also need the couplings of the Standard Model fermions to both the
new gauge bosons and the gauge bosons of the Standard Model. The relevant couplings taken from [8]
are given in Table 1.
Table 1: Couplings of the fermions to the gauge bosons of the Little Higgs model.
The electric charge of a fermion,
f, is
Qf in a notation where the change of
the electron is -1. The weak isospin of a particle is
tf3 which
is 1/2 for up type quarks and neutrinos and -1/2 for down type quarks and
charged leptons. The new Yukawa couplings are
yu=-2/5 and
ye=3/5.
It is also useful to define
xL=
l12/(
l12+
l22)
for the coupling to top quarks [
8].
- We then need to calculate the total widths of the new gauge bosons. We will
only be considering two body decays in which case the partial width for
a particular decay mode can be written as
where
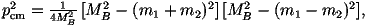 MB is the mass of the decaying gauge boson, m1,2 are the masses of
the decay products and |M|2 is the matrix element squared.
MB is the mass of the decaying gauge boson, m1,2 are the masses of
the decay products and |M|2 is the matrix element squared.
If we start with the fermion-antifermion modes then the matrix element is given by
The colour factor C is 3 if the decay products are quarks and 1 if they
are leptons.
Using the formulae and couplings in this section you should be able to
write a subroutine which has the input Standard Model and Little Higgs parameters.
This routine will then take the parameters and calculate the remaining Standard
Model couplings, Little Higgs couplings, vacuum expectation values,
particle masses and total widths.
An example program is described in Appendix B.5 and
Table 4 should give you an idea about which parameters
you need to calculate.
B ../code
This appendix describes the various pieces of code which are supplied
as either examples of how to code particular pieces of the generator
or as utilities help with writing the generator. These are all available from
A Makefile is also supplied which should build any of the example programs described in the text.
The program random.f
contains the random number generator
from the HERWIG Monte Carlo event generator together with some other useful
routines. A brief description of the routines and their arguments can be
found in Table 2 or by looking at the code.
| Name |
Type |
Use |
Arguments |
| RANGEN |
Function |
Returns a random number |
Dummy integer |
| |
|
between 0 and 1 |
|
| RANSET |
Function |
Allows the setting of the seeds |
Two integer seeds |
| |
|
(function output is a dummy) |
|
| RANGET |
Function |
Returns the current seeds |
|
| |
|
(function output is a dummy, |
Two integer seeds |
| |
|
arguments are output seeds) |
|
| RANINT |
Function |
Returns a random integer |
Dummy integer, |
| |
|
|
lower and upper limits |
| |
|
|
(integer) |
| RANUNI |
Function |
Returns a random double |
Dummy integer, |
| |
|
|
lower and upper limits |
| |
|
|
(double precision) |
Table 2: Subroutines and functions in the file
random.f together
with their uses and arguments.
B.2 Les Houches Run Common Block
The Les Houches run common block controls the information which is the same for all
the events, for example the beam energies. The common block can be found below.
C--Les Houches run common block
INTEGER MAXPUP
PARAMETER(MAXPUP=100)
INTEGER IDBMUP,PDFGUP,PDFSUP,IDWTUP,NPRUP,LPRUP
DOUBLE PRECISION EBMUP,XSECUP,XERRUP,XMAXUP
COMMON /HEPRUP/ IDBMUP(2),EBMUP(2),PDFGUP(2),PDFSUP(2),
& IDWTUP,NPRUP,XSECUP(MAXPUP),XERRUP(MAXPUP),
& XMAXUP(MAXPUP),LPRUP(MAXPUP)
The information you will need for simple processes is described in the main text.
More detailed information can be found in [7].
The block of code pdf.F, contains a
simple subroutine to calculate the PDFs. It uses the
internal PDFs from PYTHIA, HERWIG or PDFLIB to calculate the PDFs.
The main subroutine PDF takes as inputs the scale at which
the PDFs should be evaluated and the momentum fractions of the
two incoming partons. It returns an array DISFB(13,2)
which contains the parton distribution functions. The
first argument gives the type of parton, see Table 3, and
the second index gives the beam particle. There are also dummy subroutines
in case PDFLIB is not used.
| Code |
Particle |
Code |
Particle |
| 1 |
d |
7 |
d_ |
| 2 |
u |
8 |
u_ |
| 3 |
s |
9 |
s_ |
| 4 |
c |
10 |
c_ |
| 5 |
b |
11 |
b_ |
| 6 |
t |
12 |
t_ |
| 13 |
g |
|
|
Table 3: Particle codes in PDF routine.
The code may be compiled with a number of options:
-
-DPYTHIA use PYTHIA default PDFs;
- -DHERWIG use HERWIG default PDFs;
- -DPDFLIB use PDFLIB.
In each case the correct code must be linked. This means a version of either HERWIG
or PYTHIA with the dummy PDFLIB routines PDFSET and STRUCTM removed.
The file Zgen1.f contains an example program and the beginning of the subroutine
to calculate the weights for the events. The main program only sets the
beam properties in the Les Houches run common block, some simple phase-space
cuts and which type of final-state fermions to generate.
The file little.f contains a subroutine which uses the parameters
of the Standard Model and Little Higgs model to calculate the couplings,
masses and widths needed to simulate the Little Higgs model as described in
Appendix A. The parameters are explained in the code
and the parameters and couplings etc. placed in the common block LHIGGS
given below. The variables in the common block are described in Table 4.
C--common block with Liggle Higgs parameters
DOUBLE PRECISION MW,MZ,MF,ALPHA,SW,MT,FH,THETA,THETAP,G,GP,E,PI,
& CW,VEV,VEVP,ST,CT,STP,CTP,LAM,MZH,MWH,MAH,GL,GR,WIDTH
COMMON /LHIGGS/MW,MZ,MF(12),ALPHA,SW,MT,FH,THETA,THETAP,G,GP,E,PI,
& CW,VEV,VEVP,ST,CT,STP,CTP,
& LAM(2),MZH,MWH,MAH,GL(14,6),GR(14,6),WIDTH(6)
| Variable |
Type |
Input/ |
Description |
| |
|
Output |
|
| MW |
Double |
Input |
Mass of the W boson |
| MZ |
Double |
Input |
Mass of the Z boson |
| MF(12) |
Double |
Input |
Masses of the SM fermions |
| |
|
|
(1-6 are the leptons e,ne,µ,nµ,t,nt |
| |
|
|
7-12 are the quarks u, d, s, c, b, t) |
| ALPHA |
Double |
Input |
Electromagnetic Coupling Constant |
| SW |
Double |
Input |
sinqW |
| MT |
Double |
Input |
Mass of heavy top Quark |
| FH |
Double |
Input |
Symmetry breaking scale |
| THETA |
Double |
Input |
Mixing angle for SU(2) groups, q |
| THETAP |
Double |
Input |
Mixing angle for U(1) groups, q' |
| G |
Double |
Output |
Weak coupling |
| GP |
Double |
Output |
SM U(1) coupling |
| E |
Double |
Output |
Electric charge |
| PI |
Double |
Output |
p |
| CW |
Double |
Output |
cosqW |
| VEV |
Double |
Output |
Standard Model VEV ,v |
| VEVP |
Double |
Output |
New VEV , v' |
| ST |
Double |
Output |
sinq |
| CT |
Double |
Output |
cosq |
| STP |
Double |
Output |
sinq' |
| CTP |
Double |
Output |
cosq' |
| LAM(2) |
Double |
Output |
top quark Yukawa couplings, l1,2 |
| MZH |
Double |
Output |
Heavy Z mass, MZH |
| MWH |
Double |
Output |
Heavy W mass, MWH |
| MAH |
Double |
Output |
Heavy Photon Mass, MAH |
| GL(14,6) |
Double |
Output |
Left couplings of the fermion, gL |
| |
|
|
(1-6 are the leptons e,ne,µ,nµ,t,nt |
| |
|
|
7-12 are the quarks u, d, s, c, b, t |
| |
|
|
13-14 relates to the heavy top TT and Tt) |
| |
|
|
(second index 1-6 is g, Z, AH, ZH, W, WH) |
| GR(14,6) |
Double |
Output |
Right couplings of the fermion, gR |
| |
|
|
(1-6 are the leptons e,ne,µ,nµ,t,nt |
| |
|
|
7-12 are the quarks u, d, s, c, b, t |
| |
|
|
13-14 relates to the heavy top TT and Tt) |
| |
|
|
(second index 1-6 is g, Z, AH, ZH, W, WH) |
| WIDTH(6) |
Double |
Output |
Widths of the gauge bosons |
| |
|
|
(1-6 is g, Z, AH, ZH, W, WH) |
Table 4: Parameters in the LHIGGS common block.
The program in the file Zgen2.f is designed to calculate the phase-space part
of the weight using the techniques described to smooth the resonant phase space.
This program will need the code from little.f to calculate the properties of the particles, the random number generators in random.f and the code in pdf.F to calculate the PDFs. As it is using one of the PDFs from PDFLIB it must also be linked to CERNLIB.
It can be compiled using the command7
f77 Zgen2.f little.f random.f pdf.F -DPDFLIB `cernlib pdflib804 mathlib`
If you do not have PDFLIB you can instead specify the default Monte Carlo PDFs
by setting PDFGUP(1,2) = -1, PDFSUP(1,2) = -1 in the main program,
replacing DPDFLIB with DPYTHIA or DHERWIG and linking
with the appropriate generator.8
The program in the file Zgen3.f is designed to calculate both the phase space and
matrix element parts of the weight. It needs the simple histogramming package
gbook
in addition to the same programs and compilation options
as Zgen2.f.
The file boost.f contains some simple routine for Lorentz transformations taken
from HERWIG. The routines are described in Table 5.
| Name |
Type |
Use |
| BSTLOB |
Subroutine |
Transforms PI in rest frame |
| |
|
of PS to PF in the lab frame |
| BSTLOF |
Subroutine |
Transforms PI in lab |
| |
|
to PF in the rest frame of PS |
| BSTLB4 |
Subroutine |
Performs the same task as |
| |
|
BSTLOB but PI and PF are 4 not 5 vectors |
| BSTLF4 |
Subroutine |
Performs the same task as |
| |
|
BSTLOF but PI and PF are 4 not 5 vectors |
Table 5: Subroutines in the file
boost.f.
B.9 Les Houches Event Common block
The Les Houches event common block contains the information specific to a given event.
The common block can be found below.
C--Les Houches Event Common Block
INTEGER MAXNUP
PARAMETER (MAXNUP=500)
INTEGER NUP,IDPRUP,IDUP,ISTUP,MOTHUP,ICOLUP
DOUBLE PRECISION XWGTUP,SCALUP,AQEDUP,AQCDUP,PUP,VTIMUP,SPINUP
COMMON/HEPEUP/NUP,IDPRUP,XWGTUP,SCALUP,AQEDUP,AQCDUP,
& IDUP(MAXNUP),ISTUP(MAXNUP),MOTHUP(2,MAXNUP),
& ICOLUP(2,MAXNUP),PUP(5,MAXNUP),VTIMUP(MAXNUP),
& SPINUP(MAXNUP)
The information you will need for simple processes is described in the main test.
More detailed information can be found in [7].
The program Zgen4.f is a full parton-level generator.
It needs the same code as Zgen3.f.
The program Zgen5.f is a full parton-level generator
ready to interface to either HERWIG or PYTHIA.
It needs the same code as Zgen3.f and one of the
general purpose generators.
References
- [1]
-
G. Corcella et. al., HERWIG 6: An Event Generator for
Hadron Emission Reactions with Interfering Gluons (including
supersymmetric processes), JHEP 01 (2001) 010,
[http://arXiv.org/abs/hep-ph/0011363].
- [2]
-
G. Corcella et. al., HERWIG 6.5 Release Note,
hep-ph/0210213.
- [3]
-
T. Sjostrand et. al., High-Energy-Physics Event Generation
with PYTHIA 6.1, Comput. Phys. Commun. 135 (2001) 238--259,
[http://arXiv.org/abs/hep-ph/0010017].
- [4]
-
T. Sjostrand, L. Lonnblad, and S. Mrenna, PYTHIA 6.2: Physics and
Manual,
http://arXiv.org/abs/hep-ph/0108264.
- [5]
-
Particle Data Group Collaboration, K. Hagiwara et. al., Review
of particle physics, Phys. Rev. D66 (2002) 010001.
- [6]
-
H. Plothow-Besch, PDFLIB: A Library of all available Parton
Density Functions of the nucleon, the pion and the photon and the
corresponding as calculations, Comput. Phys. Commun. 75
(1993) 396--416.
- [7]
-
E. Boos et. al., Generic User Process Interface for Event
Generators, hep-ph/0109068.
- [8]
-
T. Han, H. E. Logan, B. McElrath, and L.-T. Wang, Phenomenology of the
Little Higgs model, Phys. Rev. D67 (2003) 095004,
[hep-ph/0301040].
- 1
- As the Monte Carlo event generators are
leading-order programs we should use a leading-order PDF set
and this is the most recent leading-order set available in PDFLIB.
- 2
- We can use the same formula for the photon using zero mass and width.
- 3
- In practice there are no incoming top quarks but it is easier to let the loop run over all six cases than have a special case for top.
- 4
- The quarks are 1-6, for d, u, s, c, b, t and -1,-6 for
the corresponding antiquarks. Similarly for the leptons 11-16 is e,ne,µ,nµ,t,nt and -11,-16 for the antiparticles.
- 5
- These options only differ in
which processes they select if there is more than one and are therefore
identical if there is only one process as in our case.
- 6
- In practice we are not interested in the Higgs sector and therefore
we will not set these parameters.
- 7
- On some older systems the library pdflib804 should be replaced by pdflib
- 8
- The generators also contain
dummy versions of the PDFLIB routines STRUCTM and PDFSET which should be
deleted before compiling the generator.
This document was translated from LATEX by
HEVEA.
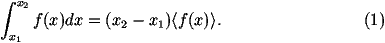
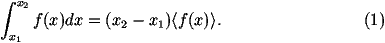
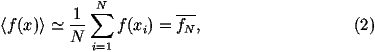
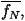 of the average. This method
is particularly
useful as we can also calculate an error on the estimate by computing
the standard
deviation and applying the central limit theorem
of the average. This method
is particularly
useful as we can also calculate an error on the estimate by computing
the standard
deviation and applying the central limit theorem

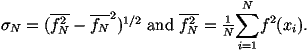

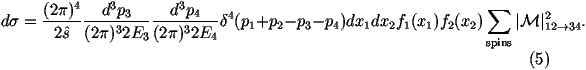
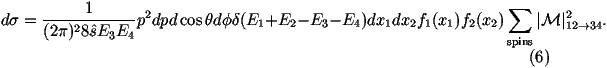
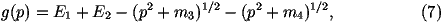
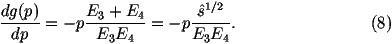
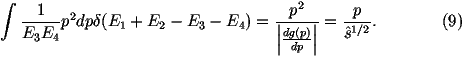
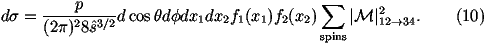
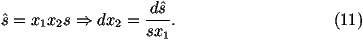
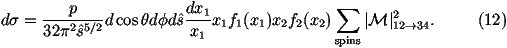



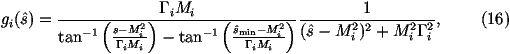
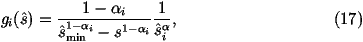
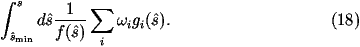
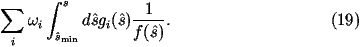

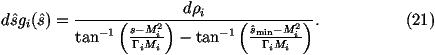
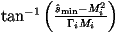 and
and
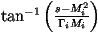 .
The value of
s^ can be calculated from ri using
.
The value of
s^ can be calculated from ri using


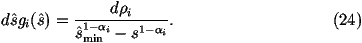





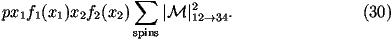
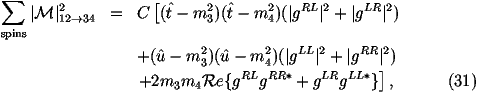
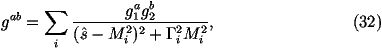
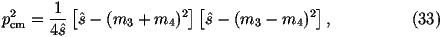

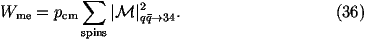


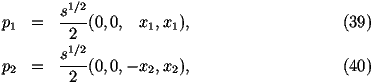
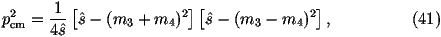
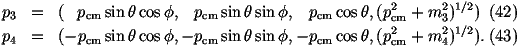
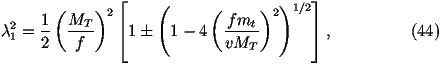
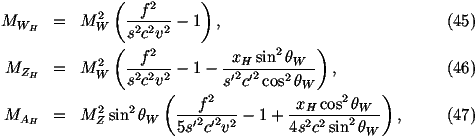
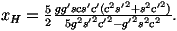
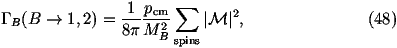
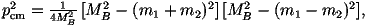 MB is the mass of the decaying gauge boson, m1,2 are the masses of
the decay products and |M|2 is the matrix element squared.
MB is the mass of the decaying gauge boson, m1,2 are the masses of
the decay products and |M|2 is the matrix element squared.